 por vinicius reis » Sex Mar 18, 2011 16:01
por vinicius reis » Sex Mar 18, 2011 16:01
o perimetro de um triangulo de lados inteiros e igual a 12m.o maior valor possivel para um dos lados deste triagulo tem medida igual a???
-
vinicius reis
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sáb Mar 12, 2011 13:49
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso tecnico
- Andamento: cursando
 por Renato_RJ » Sex Mar 18, 2011 16:58
por Renato_RJ » Sex Mar 18, 2011 16:58
Vamos chamar os lados do nosso triângulo de a,b,c e tenhamos a > b > c, logo o seu perímetro será 2p = a + b + c.
Partindo da definição, sabemos que, para a existência de um triângulo, cada lado deve ser maior que a diferença mas menor do que a soma dos outros lados, isto é:
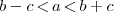
Refazendo a equação do perímetro, teremos:

Assim teremos:
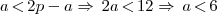
Logo, o maior valor possível para a será 5, pois estamos no domínio dos inteiros.
Espero ter ajudado..
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo]Alguém me ajuda nessa questão de calculo pfv.
por moeni » Seg Abr 04, 2022 21:54
- 0 Respostas
- 6493 Exibições
- Última mensagem por moeni

Seg Abr 04, 2022 21:54
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4532 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Cálculo Polinômio Interpolador
 por barbara-rabello » Qui Out 22, 2015 20:07
por barbara-rabello » Qui Out 22, 2015 20:07
- 1 Respostas
- 2658 Exibições
- Última mensagem por adauto martins

Sáb Out 24, 2015 11:00
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Exercícios de Calculo
por Thomas » Seg Mai 16, 2016 16:39
- 0 Respostas
- 0 Exibições
- Última mensagem por Visitante

Qua Dez 31, 1969 22:00
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5569 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



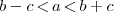

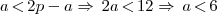

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
