 por alexandre32100 » Ter Mar 15, 2011 00:31
por alexandre32100 » Ter Mar 15, 2011 00:31
"Após percorrer uma distância de 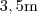 , um objeto tem sua velocidade diminuída de
, um objeto tem sua velocidade diminuída de 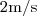 . Um segundo mais adiante, sua velocidade é diminuída novamente, mas de
. Um segundo mais adiante, sua velocidade é diminuída novamente, mas de 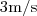 . Supondo que a aceleração seja constante em todo o movimento, calcule a velocidade no início do movimento."
. Supondo que a aceleração seja constante em todo o movimento, calcule a velocidade no início do movimento."É uma mais uma questão de física, mas basicamente trata-se de matemática.
Meu questionamento é: se há um diminuição na velocidade, há desaceleração (aceleração negativa), logo, a aceleração não pode ser constante como diz o problema.
Quem (ou o quê) está errado?
-
alexandre32100
-
 por Elcioschin » Ter Mar 15, 2011 14:38
por Elcioschin » Ter Mar 15, 2011 14:38
Pode sim: a aceleração é negativa e CONSTANTE:
|............. d = 3,5 m ............| .....................|
Vo .............. T ................. V' ..... t = 1 s ...... V"
V' - Vo - 2
V" = V' - 3 ----> V" = (Vo - 2) - 3 ----> V" = Vo - 5
No último trecho ----> V" = V' + a*t ----> Vo - 5 = (Vo - 2) + a*1 ----> a = - 3 m/s²
No primeiro trecho ----> V'² = Vo² + 2*a*d ----> (Vo - 2)² = Vo² + 2*(-3)*3,5 ----> 4 - 4*Vo = - 21 ----> Vo = 6,25 m/s²
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integrais (problemas de valor inicial)
por Anne2011 » Sex Set 16, 2011 16:26
- 4 Respostas
- 2372 Exibições
- Última mensagem por Anne2011

Sex Set 16, 2011 18:53
Cálculo: Limites, Derivadas e Integrais
-
- [Equação diferencial] Problema de valor inicial
por Aliocha Karamazov » Qua Fev 15, 2012 23:34
- 2 Respostas
- 1803 Exibições
- Última mensagem por Aliocha Karamazov

Qui Fev 23, 2012 23:43
Cálculo: Limites, Derivadas e Integrais
-
- Equações diferenciais - problema de valor inicial
por emsbp » Qui Abr 12, 2012 18:14
- 0 Respostas
- 1027 Exibições
- Última mensagem por emsbp

Qui Abr 12, 2012 18:14
Cálculo: Limites, Derivadas e Integrais
-
- [Limite no infinito]por que a expressão inicial influencia?
 por marcosmuscul » Qua Mar 27, 2013 09:41
por marcosmuscul » Qua Mar 27, 2013 09:41
- 2 Respostas
- 1358 Exibições
- Última mensagem por marcosmuscul

Qui Mar 28, 2013 11:21
Cálculo: Limites, Derivadas e Integrais
-
- [Problemas de Valor Inicial] Equações Diferenciais
por mayconf » Ter Abr 15, 2014 18:24
- 1 Respostas
- 2118 Exibições
- Última mensagem por Russman

Ter Abr 15, 2014 22:28
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
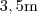 , um objeto tem sua velocidade diminuída de
, um objeto tem sua velocidade diminuída de 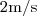 . Um segundo mais adiante, sua velocidade é diminuída novamente, mas de
. Um segundo mais adiante, sua velocidade é diminuída novamente, mas de 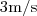 . Supondo que a aceleração seja constante em todo o movimento, calcule a velocidade no início do movimento."
. Supondo que a aceleração seja constante em todo o movimento, calcule a velocidade no início do movimento."
