 por Kelvin Brayan » Dom Mar 06, 2011 19:51
por Kelvin Brayan » Dom Mar 06, 2011 19:51
Olá pessoal, há uma questão de física sobre a qual eu tenho uma certa dúvida. Trata-se de um exercício quantitativo, ou seja, envolve cálculos matemáticos.
Não estou conseguindo resolver tal questão. No entanto, eu sei pela teoria que cargas elétricas puntiformes de mesmo sinal repelem-se.
Veja:
03.(UFPE) Quatro cargas elétricas puntiformes, de intensidades Q e q, estão fixas nos vértices de um quadrado, sabendo que as cargas Q estão nos vértices 1 e 3 e as cargas q nos vértices 2 e 4. Determine a razão Q/q para que a força sobre cada uma das cargas Q seja nula.
Fórmula:
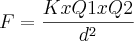
A resposta final é
![-2\sqrt[2]{2} -2\sqrt[2]{2}](/latexrender/pictures/304901268dcb59562de386577264462a.png)
-
Kelvin Brayan
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Dom Fev 20, 2011 16:50
- Localização: Varginha - MG
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Inglês
- Andamento: cursando
 por Neperiano » Sex Out 28, 2011 15:11
por Neperiano » Sex Out 28, 2011 15:11
Ola
O que você tentou fazer?
Trata-se de uma questão de eletrecidade
Nos mostre que poderemos ajudar
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Igor Mirandola » Sex Out 28, 2011 22:57
por Igor Mirandola » Sex Out 28, 2011 22:57
03.(UFPE) Quatro cargas elétricas puntiformes, de intensidades Q e q, estão fixas nos vértices de um quadrado, sabendo que as cargas Q estão nos vértices 1 e 3 e as cargas q nos vértices 2 e 4. Determine a razão Q/q para que a força sobre cada uma das cargas Q seja nula.
Fórmula:
F = K q Q / d²
Se Q e q tiverem mesmo sinal, todas as cargas vão se repelir uma das outras, e portanto, a força nunca será nula. Provavelmente Q e q vão ter sinais contrários. É a única forma de haver um equilíbrio de forças. Já podemos afirmar, portanto e sem medo, que Q/q é sempre negativo.
Antes de tudo quero dar nume as cargas, será A, B, C e D, onde a carga A está no vértice 1, a carga B está no vertice 2, a carga C está no vértice 3 e a carga D está no vértice 4.
Vamos pensar somente na carga A. Vamos colocar o quadrado num plano cartesiano tal que A esteja na origem do meu plano. Podemos escrever as coordenadas das minhas cargas como sendo:
A = (0,0)
B = (d,0)
C = (d,d)
D = (0,d)
Com isso via GA é muito facil determinar qual é a distancia entre as cargas, bastando encontrar o modulo dos vetores convenientes. Note que o vetor AC tem módulo, por definição, |AC| =
![\sqrt[2]{{d}^{2}+{d}^{2}} = \sqrt[2]{2}.d \sqrt[2]{{d}^{2}+{d}^{2}} = \sqrt[2]{2}.d](/latexrender/pictures/45c91b5e43b809d2ed7b08b53600e2f8.png)
. Pode ser dele que vem a raiz quadrada da resposta.
Mas o grande problema não é esse.
É estudar as forças que atuam em uma carga qualquer.
Vamos estudar a carga A e ver se só estudando ela conseguimos chegar em Q/q. Ela recebe influencia de tres forças neste sistema: a força elétrica das cargas B,C e D.
B e D é facil determinar porque B está no eixo x e D está no eixo y, basta aplicar a formula.
O problema é a força C, que está na diagonal neste referencial! Resolver problemas de vetores na diagonal é relativamente simples: decomponha o vetor nos eixos, utilizando ferramentas de GA, mais precisamente, projeção ortogonal, e realize as analises tanto para o eixo x quanto para o eixo y.
Será mais ou menos assim:
Vamos supor que q > 0 e Q < 0, assim, entre as cargas A e D há atração,A e B há atração, e A e C há repulsão. Observe que se q <0 e Q>0, também teriamos a mesma situação. Dessa forma, para haver equilibrio a somatória de todas as forças deve ser zero. São três forças que podemos decompor nos eixos x e y, e assim, para haver equilivrio, a somatória de todas as forças em cada eixo deve ser zero.
Antes de mais nada vamos dar nomes as variaveis força. Força que B exerce em A, vamos chamar de Fb. A força que C exerce em A vamos chamar de Fc, e a força que D exerce em A, vamos chamar de Fd.
Agora, vamos pensar no eixo x, e ver se apartir dele chegamos na tão esperada razão Q/q:
Por hipótese, há equilibrio, e portanto, força da carga B + Força da carga C decomposta no eixo x = 0
Analisando o sinal das forças, a força B está no sentido positivo de x, por causa da atração. A força C em x está no sentido negativo de x. Podemos então escrever que
|Fb| - |Fc x| = 0 e portanto, |Fb| = |Fc em x|
Para de decompor a força Fc no eixo x, basta conhecer o angulo da diagonal, sabemos que vale pi/4
Fc x = Fc sen(pi/4)
Fc x = Fc
![\frac{\sqrt[2]{2}}{2} \frac{\sqrt[2]{2}}{2}](/latexrender/pictures/087ef0498ec0056debd92518bfa3944e.png)
Assim, aplicando a formula no eixo x, temos que,
|Fb| = |Fc em x|
![\frac{kQq}{d²} = \frac{kQ²}{{\left(d \sqrt[2]{2} \right)}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{kQq}{d²} = \frac{kQ²}{2{d}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{q}{1} = \frac{Q}{2} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \frac{\sqrt[2]{2}}{\sqrt[2]{2}} \Rightarrow 2\sqrt[2]{2} \frac{kQq}{d²} = \frac{kQ²}{{\left(d \sqrt[2]{2} \right)}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{kQq}{d²} = \frac{kQ²}{2{d}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{q}{1} = \frac{Q}{2} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \frac{\sqrt[2]{2}}{\sqrt[2]{2}} \Rightarrow 2\sqrt[2]{2}](/latexrender/pictures/b5d8e837279a202348d3f86a4449e81d.png)
Obersve que encontramos Q/q em módulo. Falta fazer a análise do sinal, aliás, ja foi feito, para que hava equilíbrio q>0 e Q<0... ou q<0 e Q>0, é por isso que Q/q < 0 sempre!
A resposta fica - 2 raiz 2
-
Igor Mirandola
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Out 28, 2011 21:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão de Física
por valeuleo » Sáb Mai 28, 2011 16:03
- 2 Respostas
- 3030 Exibições
- Última mensagem por valeuleo

Sáb Mai 28, 2011 16:29
Funções
-
- Física
por Mi_chelle » Qua Abr 13, 2011 17:52
- 3 Respostas
- 5030 Exibições
- Última mensagem por Mi_chelle

Qui Abr 14, 2011 00:07
Números Complexos
-
- física
 por leticiapires52 » Sáb Mar 28, 2015 20:10
por leticiapires52 » Sáb Mar 28, 2015 20:10
- 0 Respostas
- 1195 Exibições
- Última mensagem por leticiapires52

Sáb Mar 28, 2015 20:10
Estatística
-
- Calculo de fisica
 por andersontricordiano » Sex Jul 01, 2011 17:13
por andersontricordiano » Sex Jul 01, 2011 17:13
- 1 Respostas
- 1903 Exibições
- Última mensagem por Neperiano

Sex Jul 01, 2011 18:40
Física
-
- Fisica Cinemática
por GABRUEL » Qua Jul 13, 2011 17:08
- 8 Respostas
- 5753 Exibições
- Última mensagem por GABRUEL

Qui Jul 14, 2011 15:34
Física
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
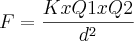
![-2\sqrt[2]{2} -2\sqrt[2]{2}](/latexrender/pictures/304901268dcb59562de386577264462a.png)


![\sqrt[2]{{d}^{2}+{d}^{2}} = \sqrt[2]{2}.d \sqrt[2]{{d}^{2}+{d}^{2}} = \sqrt[2]{2}.d](/latexrender/pictures/45c91b5e43b809d2ed7b08b53600e2f8.png) . Pode ser dele que vem a raiz quadrada da resposta.
. Pode ser dele que vem a raiz quadrada da resposta.![\frac{\sqrt[2]{2}}{2} \frac{\sqrt[2]{2}}{2}](/latexrender/pictures/087ef0498ec0056debd92518bfa3944e.png)
![\frac{kQq}{d²} = \frac{kQ²}{{\left(d \sqrt[2]{2} \right)}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{kQq}{d²} = \frac{kQ²}{2{d}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{q}{1} = \frac{Q}{2} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \frac{\sqrt[2]{2}}{\sqrt[2]{2}} \Rightarrow 2\sqrt[2]{2} \frac{kQq}{d²} = \frac{kQ²}{{\left(d \sqrt[2]{2} \right)}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{kQq}{d²} = \frac{kQ²}{2{d}^{2}} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{q}{1} = \frac{Q}{2} \frac{\sqrt[2]{2}}{2} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \Rightarrow \frac{Q}{q} = \frac{4}{\sqrt[2]{2}} \frac{\sqrt[2]{2}}{\sqrt[2]{2}} \Rightarrow 2\sqrt[2]{2}](/latexrender/pictures/b5d8e837279a202348d3f86a4449e81d.png)
