CALCULO DE INTEGRAL

[Jaison Werner]

QUAL O VALOR DE , com n=6 PELA REGRA DE SIMPSON? CONSIDERE 4 CASAS DECIMAIS.

RESPOSTA: 4,6678

[Prof lucio Baptista]

ESTE MÉTODO É U, OU SEJA, QUANDO SE QUER OBTERTILIZADO PARA INTERVALO EM QUE O NÚMERO DE SUBINTERVALOS n É MULTIPLO DE 2 UMA FÓRMULA PARA INTEGRAR f(X)ENTRE TRES PONTOS CONSECUTIVOS ,, .

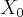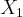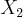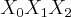A FÓRMULA É OBTIDA APROXIMANDO-SE A FUNÇÃO f(x) POR UM POLINÔMIO INTERPOLADOR DE 2º GRAU PARA ESTA APROXIMAÇÃO SÃO NECESSÁRIOS TRÊS PONTOS , QUE DEVERÃO ESTAR IGUALMENTEESPAÇADOS. CHEGANDO A SEGUINTE FÓRMULA:

A= .[+++++...++].

OS VALORES DOS COEFICIENTES QUE COMPÕEM ESTE MÉTODO ESTÃO DISPOSTOS DE MANEIRA QUE INICIALMENTE O VALOR É 1, OS SUBSEQUENTES SÃO 4 E 2 NA SEQUENCIA E FINALIZA COM 1.

VOU DAR UM EXEMPLO:

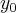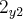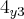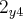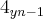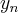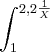CALCULAR A INTEGRAL dx COM N= 6.

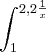SOLUÇÃO: dx= 1ntal que x 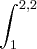= 1n tal que 2,2 tal que - 1n tal que 1 talque= 0,7885 - 0 = 0,7885
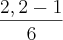h= ()=0,2

ENTÃO SH. JAISOM O VALOR DA SUA INTEGRAL É:4,6678

´ISSO NÃO SENHORA FANTINE?

[MarceloFantini]

Primeiro, é senhor Fantini, sou homem. E segundo, não sei, não aprendi a matéria com a qual estão lidando (suponho que seja Cálculo Numérico?).

[Jaison Werner]

É calculo numérico sim fantini,não sabe?

[MarceloFantini]

Vou ter esse semestre, se a dúvida estiver em aberto tentarei.