 por malbino » Sex Nov 26, 2010 19:19
por malbino » Sex Nov 26, 2010 19:19
Estou com um problema, pois preciso aplicar um percentual de 0,0837 nos valores abaixo:
7,11 + 5,22 = 12,33
7,11 * 0,0837 = 0,595107 = 0,60
5,22 * 0,0837 = 0,436914 = 0,44
12,33 * 0,0837 = 1,032021 = 1,03
Devido o arredondamento, quando somo os valores não bate com o total.
0,60 + 0,44 = 1,04
Gostaria de saber se existe alguma fórmula para resolver este probema de arredondamento.
-
malbino
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 26, 2010 18:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologo em Processamento de Dados
- Andamento: formado
 por victoreis1 » Sex Nov 26, 2010 19:35
por victoreis1 » Sex Nov 26, 2010 19:35
basta deixar pra arredondar no final.. pra quê a pressa?
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sex Nov 26, 2010 20:23
por MarceloFantini » Sex Nov 26, 2010 20:23
Concordo com o victor, e apenas lembrando que normalmente quando a casa anterior é menor que cinco, arredondamos para baixo, e quando maior ou igual a cinco para cima (a casa anterior à quantidade de casas referentes a precisão desejada).
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por malbino » Sáb Nov 27, 2010 16:00
por malbino » Sáb Nov 27, 2010 16:00
Na minha solução eu tenho que apresentar todos os valores com 2 casas decimais. Eu poderia jogar a diferença no segundo valor, mas eu queria saber se tem uma fórmula matemática para isso, pois o meu problema é mais complexo que o exemplo que apresentei, pois com a solução que vcs deram o meu trabalho seriabem maior.
-
malbino
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Nov 26, 2010 18:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologo em Processamento de Dados
- Andamento: formado
 por MarceloFantini » Sáb Nov 27, 2010 16:32
por MarceloFantini » Sáb Nov 27, 2010 16:32
Eu apenas mudaria um dos seus valores: de
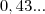
para
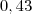
, seguindo a regra que eu falei.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Arredondamento
por acuria » Ter Set 20, 2011 08:33
- 4 Respostas
- 1742 Exibições
- Última mensagem por MarceloFantini

Ter Set 20, 2011 18:41
Álgebra Elementar
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10728 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9739 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3325 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4620 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





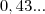 para
para 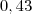 , seguindo a regra que eu falei.
, seguindo a regra que eu falei.