Preciso determinar se a seguinte série converge:

Comecei utilizando o teste da integral:
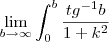
Ok. Observando, lembrei que se utiliza-se a ideia de que:
![\int_{}^{} \frac{dx}{\sqrt[]{1+{x}^{2}}} \int_{}^{} \frac{dx}{\sqrt[]{1+{x}^{2}}}](/latexrender/pictures/29bee737b38bc71589ef2c8c8999443e.png)
e nela podemos usar uma substituição trigonométrica.
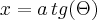
Ou seja, a equação poderia ser descrita como:
} \lim_{b\rightarrow\infty} \int_{0}^{b} \frac{{tg}^{-1} b}{\sqrt[]({}1+{b}^{4})}](/latexrender/pictures/89ae8a6102996430f0724d5bf0ccad0a.png)
Substituindo:
![{x}^{2} = tg(\Theta)\, ,x = \sqrt[]{tg(\Theta)}\, ,d({x}^{2}) = {sec}^{2}(\Theta) {x}^{2} = tg(\Theta)\, ,x = \sqrt[]{tg(\Theta)}\, ,d({x}^{2}) = {sec}^{2}(\Theta)](/latexrender/pictures/d82b05acd82cb77f630e197f5886e93d.png)
Ou seja,
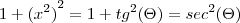
ATENÇÃO AGORA. Fiz de dois jeitos distintos, pois fiquei na dúvida. Vejam se algum confere, por favor:
JEITO A
Voltando a primeira integral:

Seguindo:
![\int_{}^{} arctg(\Theta)= arccotg (\Theta) + ln\,\sqrt[]{2} + C \int_{}^{} arctg(\Theta)= arccotg (\Theta) + ln\,\sqrt[]{2} + C](/latexrender/pictures/32a6d0a1b1e2038805a8d6198d85f969.png)
Limite:
![\lim_{b\rightarrow\infty} arccotg (b) + ln\,\sqrt[]{2} \lim_{b\rightarrow\infty} arccotg (b) + ln\,\sqrt[]{2}](/latexrender/pictures/516ab18989298efec4ad2a8345511fa3.png)
O jeito B também não confere com o resultado final.
RESULTADO FINAL:
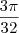
Acho que fiz uma tempestade em um copo d'água. A resolução deve ser muito mais simples, mas não consigo vê-la. Alguém pode me ajudar?
Obrigado!


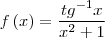 e começaria a trabalhar a partir dela
e começaria a trabalhar a partir dela
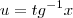
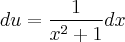 que é exatamente o que temos em nossa integral, substituindo fica
que é exatamente o que temos em nossa integral, substituindo fica 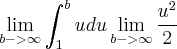 voltando p/u e aplicando os limites fica
voltando p/u e aplicando os limites fica 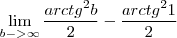


 ao
ao  é injetora e sobrejetora (podemos ver esboçando o gráfico) . Assim , a função arco tangente (inversa da tangente) está bem definida de
é injetora e sobrejetora (podemos ver esboçando o gráfico) . Assim , a função arco tangente (inversa da tangente) está bem definida de 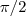 e inferiormente por
e inferiormente por 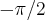 e assim ela é limitada por
e assim ela é limitada por  para todo
para todo  . Quando multiplicamos está desigualdade por
. Quando multiplicamos está desigualdade por  obtemos que
obtemos que 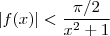 . Desta forma , para
. Desta forma , para 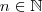 , pondo
, pondo 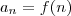 temos
temos 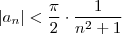 .Pelo que
.Pelo que 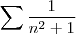 converge ,então
converge ,então  converge .Logo ,
converge .Logo , 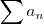 converge .
converge .
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)