-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478483 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 533125 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 496637 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 709493 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2128130 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por adauto martins » Ter Abr 27, 2021 10:51
por adauto martins » Ter Abr 27, 2021 10:51
(ITA-1957)sabendo-se que
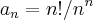
, calcular
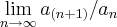
.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Ter Abr 27, 2021 11:00
por adauto martins » Ter Abr 27, 2021 11:00
soluçao
tomemos
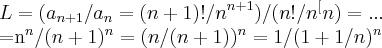
usando o
limite fundamental
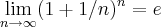
teremos
para
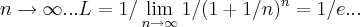
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Polinomio exercio II
por MarianaAlmeida » Qui Jul 09, 2009 16:51
- 1 Respostas
- 3257 Exibições
- Última mensagem por Cleyson007

Sáb Jul 11, 2009 08:48
Polinômios
-
- Dúvida em exercío sobre segmentos de retas.
por Danilo » Sáb Abr 21, 2012 21:33
- 1 Respostas
- 1999 Exibições
- Última mensagem por Danilo

Seg Abr 23, 2012 00:27
Álgebra Elementar
-
- NAO CVONSIGO RESOLVER ESTE EXERCIO ME AJUDEM POR FAVOR.
por weverton » Sex Mai 14, 2010 02:04
- 2 Respostas
- 2091 Exibições
- Última mensagem por weverton

Sáb Mai 15, 2010 16:13
Matemática Financeira
-
- Exercio do Intocaveis "Livro do cursinho do objetivo"
por kalong » Qua Out 24, 2012 22:29
- 3 Respostas
- 25570 Exibições
- Última mensagem por diegolopes1988

Sáb Jan 14, 2017 17:05
Álgebra Elementar
-
- exercicio resolvido
por adauto martins » Sex Jul 15, 2016 14:48
- 0 Respostas
- 14983 Exibições
- Última mensagem por adauto martins

Sex Jul 15, 2016 14:48
Teoria dos Números
Usuários navegando neste fórum: Nenhum usuário registrado e 56 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
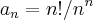 , calcular
, calcular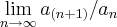 .
.
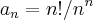 , calcular
, calcular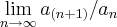 .
.
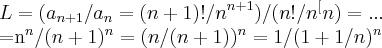
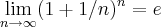
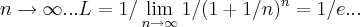

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)