 por Matheus1999 » Seg Jan 25, 2021 14:15
por Matheus1999 » Seg Jan 25, 2021 14:15
Olá, eu estou com um pouco de dúvida na resolução destas 2 derivadas, eu tentei resolve-las, mas acabo sempre por "travar".
O enunciado diz o seguinte: "Utilizando a regra das derivadas, determine o y'"
Em anexo, uma imagem contendo as derivadas.
OBS: Desculpem-me por qualquer erro, esse é o primeiro tópico que criei aqui no fórum.
- Anexos
-

-
Matheus1999
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Nov 17, 2020 04:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por DanielFerreira » Sex Abr 02, 2021 18:23
por DanielFerreira » Sex Abr 02, 2021 18:23
Olá
Matheus1999, seja bem-vindo!
Matheus1999 escreveu:Utilizando a regra das derivadas, determine o y
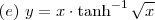
Para solucionar este item, precisamos saber que
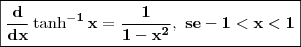
.
Seja
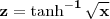
. Determinemos sua derivada considerando
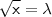
. Com efeito, implica que
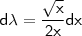
. Daí,
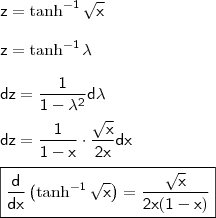
Por fim, aplicando a
regra do produto:
![\\ \mathsf{y = x \cdot \tanh^{- 1} \sqrt{x}} \\\\ \mathsf{dy = \left [ 1 \cdot \tanh^{- 1} \sqrt{x} + x \cdot \frac{\sqrt{x}}{2x(1 - x)} \right ] dx} \\\\ \mathsf{\frac{dy}{dx} = \tanh^{- 1} \sqrt{x} + \frac{\sqrt{x}}{2(1 - x)}} \\\\ \boxed{\boxed{\mathsf{\frac{d}{dx} \left ( x \cdot \tanh^{- 1} \sqrt{x} \right ) = \tanh^{- 1} \sqrt{x} + \frac{\sqrt{x}}{2(1 - x)}}}} \\ \mathsf{y = x \cdot \tanh^{- 1} \sqrt{x}} \\\\ \mathsf{dy = \left [ 1 \cdot \tanh^{- 1} \sqrt{x} + x \cdot \frac{\sqrt{x}}{2x(1 - x)} \right ] dx} \\\\ \mathsf{\frac{dy}{dx} = \tanh^{- 1} \sqrt{x} + \frac{\sqrt{x}}{2(1 - x)}} \\\\ \boxed{\boxed{\mathsf{\frac{d}{dx} \left ( x \cdot \tanh^{- 1} \sqrt{x} \right ) = \tanh^{- 1} \sqrt{x} + \frac{\sqrt{x}}{2(1 - x)}}}}](/latexrender/pictures/da2a4c0868a55abe8f710061d50cded6.png)
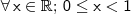
.
Quanto ao outro item, podes passar o fator que está fora da raiz para dentro e aplicar a
regra da cadeia!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo 1 - Derivadas
por johnatta » Dom Nov 22, 2015 11:40
- 1 Respostas
- 2778 Exibições
- Última mensagem por adauto martins

Qua Nov 25, 2015 16:40
Cálculo: Limites, Derivadas e Integrais
-
- [Calculo] Derivadas sucessivas
por karenfreitas » Sáb Mai 28, 2016 11:00
- 2 Respostas
- 3747 Exibições
- Última mensagem por nakagumahissao

Seg Mai 30, 2016 23:18
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 2] derivadas parciais
 por NavegantePI » Sáb Jun 25, 2016 18:08
por NavegantePI » Sáb Jun 25, 2016 18:08
- 1 Respostas
- 2654 Exibições
- Última mensagem por adauto martins

Seg Jun 27, 2016 12:22
Cálculo: Limites, Derivadas e Integrais
-
- [cálculo de derivadas] Ajuda em exercicio
por Ljoe » Ter Jul 12, 2011 12:49
- 3 Respostas
- 2740 Exibições
- Última mensagem por Fabio Cabral

Qua Jul 13, 2011 10:52
Cálculo: Limites, Derivadas e Integrais
-
- [cálculo de derivadas de funções modulares]
por letciabr7 » Sáb Mai 09, 2015 16:44
- 1 Respostas
- 1867 Exibições
- Última mensagem por adauto martins

Seg Mai 11, 2015 16:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 13 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


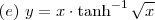
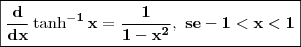 .
.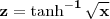 . Determinemos sua derivada considerando
. Determinemos sua derivada considerando 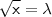 . Com efeito, implica que
. Com efeito, implica que 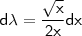 . Daí,
. Daí,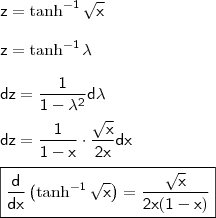
![\\ \mathsf{y = x \cdot \tanh^{- 1} \sqrt{x}} \\\\ \mathsf{dy = \left [ 1 \cdot \tanh^{- 1} \sqrt{x} + x \cdot \frac{\sqrt{x}}{2x(1 - x)} \right ] dx} \\\\ \mathsf{\frac{dy}{dx} = \tanh^{- 1} \sqrt{x} + \frac{\sqrt{x}}{2(1 - x)}} \\\\ \boxed{\boxed{\mathsf{\frac{d}{dx} \left ( x \cdot \tanh^{- 1} \sqrt{x} \right ) = \tanh^{- 1} \sqrt{x} + \frac{\sqrt{x}}{2(1 - x)}}}} \\ \mathsf{y = x \cdot \tanh^{- 1} \sqrt{x}} \\\\ \mathsf{dy = \left [ 1 \cdot \tanh^{- 1} \sqrt{x} + x \cdot \frac{\sqrt{x}}{2x(1 - x)} \right ] dx} \\\\ \mathsf{\frac{dy}{dx} = \tanh^{- 1} \sqrt{x} + \frac{\sqrt{x}}{2(1 - x)}} \\\\ \boxed{\boxed{\mathsf{\frac{d}{dx} \left ( x \cdot \tanh^{- 1} \sqrt{x} \right ) = \tanh^{- 1} \sqrt{x} + \frac{\sqrt{x}}{2(1 - x)}}}}](/latexrender/pictures/da2a4c0868a55abe8f710061d50cded6.png)
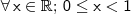 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.