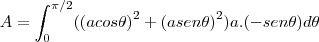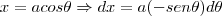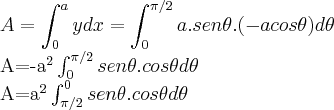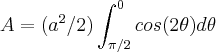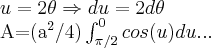por 1marcus » Dom Abr 26, 2020 16:32
por 1marcus » Dom Abr 26, 2020 16:32
Alo, então estou tendo dificuldade com estes exercícios, se poderem me ajuda agradeço,
1)qual é o valor da area total da região compreendida pelo grafico da função f(x)=sen(2x) e o eixo no intervalo [0,3?]?
2)qual é o area da região entre os gráficos de f(x)=\sqrt{x+7} e g(x)=0,5(x+7)?
3)em algumas aplicações na engenharia precisamos determinar a area de placas finas descritas por uma regiao no plano. Qual é a area da placa fina que cobre a região no primeiro quadrante pelo circilos x^{2}+y^{2}=a^{2}
-
1marcus
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Nov 02, 2018 15:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por adauto martins » Sex Mai 01, 2020 18:55
por adauto martins » Sex Mai 01, 2020 18:55
1)

fazendo-se
![u=2x\Rightarrow du=2dx
A=(1/2)\int_{u(0)}^{u(3\pi)}sen(u) du
A=(1/2).(-cosu)[0,6\pi]... u=2x\Rightarrow du=2dx
A=(1/2)\int_{u(0)}^{u(3\pi)}sen(u) du
A=(1/2).(-cosu)[0,6\pi]...](/latexrender/pictures/36d5cdb5c795feea606c93629ba7d0ce.png)
termine-o...
2)
aqui achar os pontos de intersecçao das curvas(pontos comuns)
![\sqrt[]{(x+7)}=(1/2)(x+7)\Rightarrow
x+7=(1/4)(x+7)^{2} \sqrt[]{(x+7)}=(1/2)(x+7)\Rightarrow
x+7=(1/4)(x+7)^{2}](/latexrender/pictures/61a2e0697574847166ced7956aeab1ce.png)
achando os valores de x,determina-se o intervalo de integraçao
![A=\int_{{x}_{1}}^{{x}_{2}}(1/2)(x+7)-\sqrt[]{(x+7)}dx A=\int_{{x}_{1}}^{{x}_{2}}(1/2)(x+7)-\sqrt[]{(x+7)}dx](/latexrender/pictures/125a9744a5b0836491887462d75d4f28.png)
onde

termine-o...
3)
aqui usaremos coordenadas polares


pois,

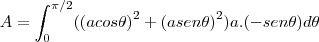
pois,
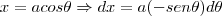
termine-o...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sáb Mai 02, 2020 14:57
por adauto martins » Sáb Mai 02, 2020 14:57
uma correçao no iem 3)
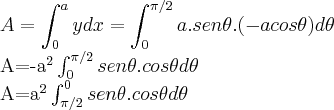
aqui usaremos a identidade trigonometrica

logo
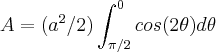
faz-se
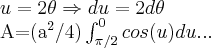
termine-o...obrigado
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercícios de cálculo 3
 por ezidia51 » Sáb Nov 09, 2019 21:27
por ezidia51 » Sáb Nov 09, 2019 21:27
- 0 Respostas
- 5039 Exibições
- Última mensagem por ezidia51

Sáb Nov 09, 2019 21:27
Cálculo: Limites, Derivadas e Integrais
-
- exercícios de cálculo 3
 por ezidia51 » Sáb Nov 09, 2019 21:32
por ezidia51 » Sáb Nov 09, 2019 21:32
- 1 Respostas
- 3010 Exibições
- Última mensagem por ezidia51

Sáb Nov 09, 2019 21:34
Cálculo: Limites, Derivadas e Integrais
-
- exercícios de cálculo 3
 por ezidia51 » Sáb Nov 09, 2019 21:39
por ezidia51 » Sáb Nov 09, 2019 21:39
- 1 Respostas
- 4168 Exibições
- Última mensagem por adauto martins

Dom Nov 10, 2019 00:29
Cálculo: Limites, Derivadas e Integrais
-
- exercícios de cálculo 3
 por ezidia51 » Dom Nov 10, 2019 15:22
por ezidia51 » Dom Nov 10, 2019 15:22
- 3 Respostas
- 7188 Exibições
- Última mensagem por adauto martins

Dom Nov 10, 2019 21:07
Cálculo: Limites, Derivadas e Integrais
-
- Exercícios Calculo I - Limite
por CloudP4 » Seg Jun 07, 2010 23:57
- 7 Respostas
- 6770 Exibições
- Última mensagem por MarceloFantini

Dom Jun 13, 2010 19:04
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![u=2x\Rightarrow du=2dx
A=(1/2)\int_{u(0)}^{u(3\pi)}sen(u) du
A=(1/2).(-cosu)[0,6\pi]... u=2x\Rightarrow du=2dx
A=(1/2)\int_{u(0)}^{u(3\pi)}sen(u) du
A=(1/2).(-cosu)[0,6\pi]...](/latexrender/pictures/36d5cdb5c795feea606c93629ba7d0ce.png)
![\sqrt[]{(x+7)}=(1/2)(x+7)\Rightarrow
x+7=(1/4)(x+7)^{2} \sqrt[]{(x+7)}=(1/2)(x+7)\Rightarrow
x+7=(1/4)(x+7)^{2}](/latexrender/pictures/61a2e0697574847166ced7956aeab1ce.png)
![A=\int_{{x}_{1}}^{{x}_{2}}(1/2)(x+7)-\sqrt[]{(x+7)}dx A=\int_{{x}_{1}}^{{x}_{2}}(1/2)(x+7)-\sqrt[]{(x+7)}dx](/latexrender/pictures/125a9744a5b0836491887462d75d4f28.png)