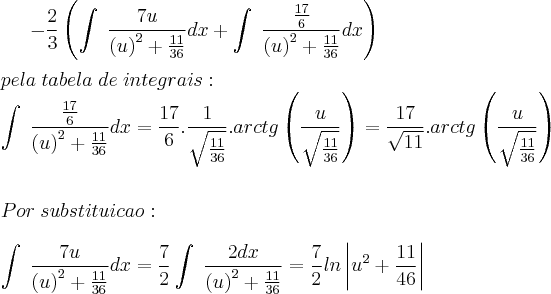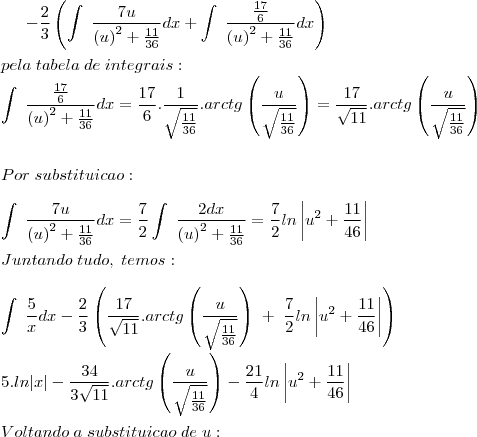por dark_slack » Sáb Dez 15, 2018 11:29
por dark_slack » Sáb Dez 15, 2018 11:29
bom dia,
quero resolver esta integral de fração parcial que não consigo achar uma solução:

Quero a atenção de todos!
Obrigado.
-
dark_slack
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Dez 13, 2018 19:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Gebe » Sáb Dez 15, 2018 22:25
por Gebe » Sáb Dez 15, 2018 22:25
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- integrais parciais
por matmatco » Seg Nov 12, 2012 00:29
- 1 Respostas
- 1377 Exibições
- Última mensagem por MarceloFantini

Seg Nov 12, 2012 05:11
Cálculo: Limites, Derivadas e Integrais
-
- integrais por frações parciais
 por engrangel » Qua Abr 18, 2012 15:46
por engrangel » Qua Abr 18, 2012 15:46
- 2 Respostas
- 2942 Exibições
- Última mensagem por engrangel

Qui Abr 19, 2012 17:47
Cálculo: Limites, Derivadas e Integrais
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8843 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas parciais
por john » Ter Fev 15, 2011 15:37
- 7 Respostas
- 6833 Exibições
- Última mensagem por john

Sáb Fev 19, 2011 16:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas parciais
por baianinha » Ter Jul 05, 2011 00:50
- 1 Respostas
- 2671 Exibições
- Última mensagem por MarceloFantini

Ter Jul 05, 2011 03:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




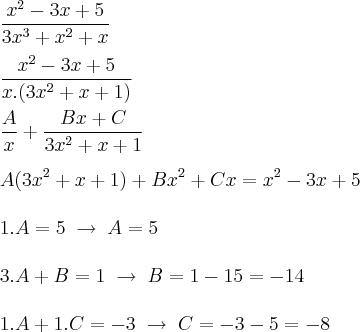
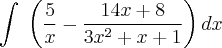
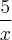 da integral é simples de resolver, vamos então nos concentrar no segundo termo:
da integral é simples de resolver, vamos então nos concentrar no segundo termo: