É bem semelhante ao feito pra uma variavel.
Quando temos uma variavel, utilizando, por exemplo, a função
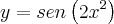
, procedemos da seguinte forma:
-> Identificamos as funções:
y(z) =
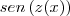
z(x) =
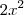
-> Aplicamos a regra da cadeia multiplicando as
derivadas de cada função identificada em relação a sua variavel correspondente:

No caso das
derivadas parciais podemos ter funções com mais de uma variavel.
Cada variavel vai definir um caminho de derivação;
Em cada um destes caminhos vamos aplicar a regra da cadeia de uma variavel e ao fim somamos os varios caminhos.
Veja o exemplo:
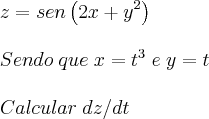
z(x,y) está em função de x e y, logo podemos ter dois caminhos de derivação.
1° caminho por x : "x" é variavel e "y" é constante.
2° caminho por y : "y" é variavel e "x" é constante.
Seja h = 2x+y²
Aplicando a regra da cadeia no 1° caminho:

Aplicando a regra da cadeia no 2° caminho:
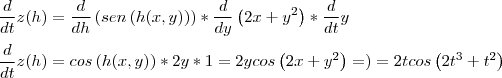
Somando-se os dois caminhos:
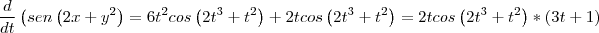
Espero que tenha ajudado, qualquer duvida deixe msg.



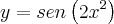 , procedemos da seguinte forma:
, procedemos da seguinte forma: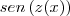
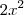

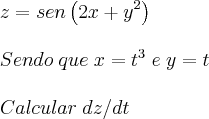

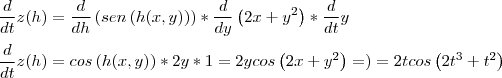
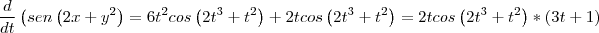


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
