seja y f x uma função dada pela implicitamente pela questao x²+xy+y² = 3. admitindo f derivavel, determine as possiveis retas tangentes ao gráfico de f que são normais à reta x-y+1=0.
Eu tentei mais n consegui começar alguem pode me ajudar a fazer



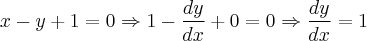
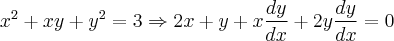
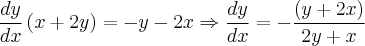
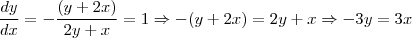


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 17 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

