-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478533 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 533534 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 497047 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 710612 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2130099 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por liviatoniolo222 » Seg Mai 21, 2018 22:54
por liviatoniolo222 » Seg Mai 21, 2018 22:54
Não estou conseguindo sair dessa questão.
? t. sec-¹(t)dt
O exercício pede para que seja feito por integração por partes
Fiz a integração usando ?udv= u.v -?vdu
e cheguei a isso
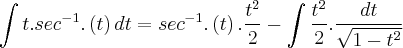
depois disso eu não soube mais o que fazer, meu professor disse que eu teria que achar a identidade trigonométrica e fazer com que t seja igual a sen (u) mas eu não entendi como e nem porquê eu devo fazer isso
- Anexos
-
-
liviatoniolo222
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mai 06, 2018 22:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: eletromecanica
- Andamento: cursando
 por Gebe » Ter Mai 22, 2018 10:26
por Gebe » Ter Mai 22, 2018 10:26
Nao lembrava mais como fazia este tipo de questão. Dei uma olhada nos meus materiais antigos na parte de substituição trigonometrica (coloco uma parte em anexo) e acho que tua questão cai no caso do primeiro exemplo do anexo, ficando assim:

Acho que é isso, mas da uma boa conferida, qualquer duvida manda msg. Espero ter ajudado, bons estudos
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por liviatoniolo222 » Ter Mai 22, 2018 16:01
por liviatoniolo222 » Ter Mai 22, 2018 16:01
Fiz a mesma pergunta em um outro fórum e me disseram que eu confundi sec-¹ com sen-¹ pois a fórmula de sen-¹ é
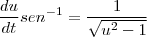
e realmente de acordo com a tabela
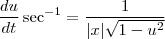
seria a fórmula correta para sec-¹
Fiquei confusa
-
liviatoniolo222
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mai 06, 2018 22:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: eletromecanica
- Andamento: cursando
 por liviatoniolo222 » Ter Mai 22, 2018 20:48
por liviatoniolo222 » Ter Mai 22, 2018 20:48
Conversando com um outro professor, ele sugeriu que usasse esse método.
Estaria correto?
- Anexos
-

-
liviatoniolo222
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Mai 06, 2018 22:54
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: eletromecanica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INTEGRAL] Integral por partes! Alguem pode me ajudar?
por mih123 » Qua Jan 16, 2013 20:18
- 3 Respostas
- 3939 Exibições
- Última mensagem por adauto martins

Qua Out 22, 2014 09:11
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por rita becher » Qua Jun 01, 2011 22:05
- 2 Respostas
- 2050 Exibições
- Última mensagem por rita becher

Qui Jun 02, 2011 10:30
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por rita becher » Qui Jun 02, 2011 00:20
- 4 Respostas
- 3578 Exibições
- Última mensagem por rita becher

Sáb Jun 04, 2011 13:01
Cálculo: Limites, Derivadas e Integrais
-
- Integral por Partes
por Guilherme Carvalho » Ter Mar 06, 2012 23:08
- 2 Respostas
- 1800 Exibições
- Última mensagem por Guilherme Carvalho

Qua Mar 07, 2012 10:39
Cálculo: Limites, Derivadas e Integrais
-
- integral por partes
por gasparina nunes » Sáb Abr 07, 2012 23:42
- 3 Respostas
- 2221 Exibições
- Última mensagem por fraol

Dom Abr 08, 2012 22:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 49 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
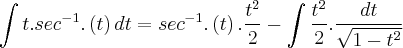




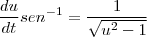
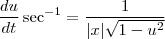 seria a fórmula correta para sec-¹
seria a fórmula correta para sec-¹ em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.