-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480296 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 540260 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 504116 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 729514 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2166911 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por leticiaeverson » Dom Abr 22, 2018 00:39
por leticiaeverson » Dom Abr 22, 2018 00:39
Calcule (df/dx ; df/dy) ,e as derivadas mistas em cada caso:
a) f(x,y)=
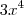
– 2xy² +
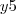
b) f(x,y)= cos²(3x) + sen²(3y)
c) f(x,y)=Ln(3x –y³)
-
leticiaeverson
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Abr 22, 2018 00:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Gebe » Dom Abr 22, 2018 03:39
por Gebe » Dom Abr 22, 2018 03:39
leticiaeverson escreveu:Calcule (df/dx ; df/dy) ,e as derivadas mistas em cada caso:
a) f(x,y)=
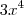
– 2xy² +
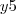
b) f(x,y)= cos²(3x) + sen²(3y)
c) f(x,y)=Ln(3x –y³)
a)
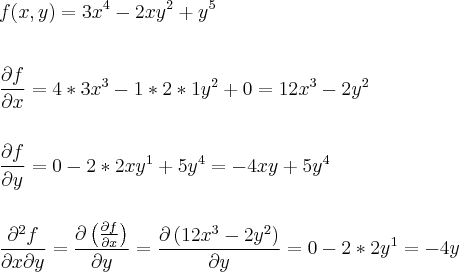
b)
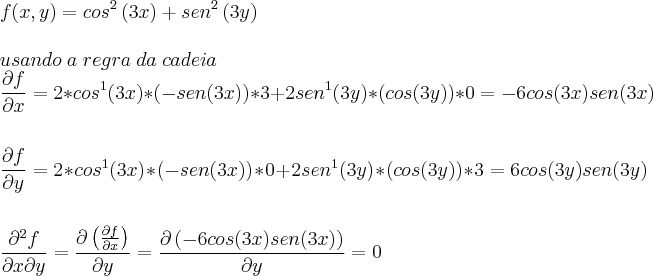
c)
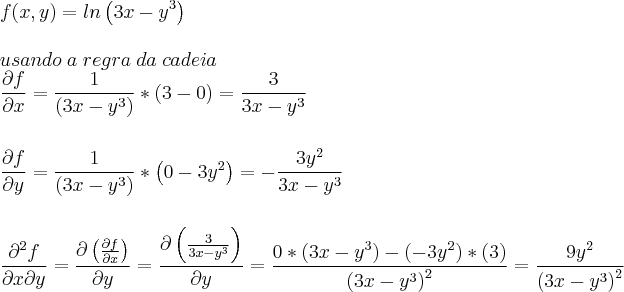
Espero ter ajudado. Se ficarem duvidas deixe msg.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por leticiaeverson » Dom Abr 22, 2018 14:46
por leticiaeverson » Dom Abr 22, 2018 14:46
Me ajudou muito! Consegui compreender bem! Obrigada!
-
leticiaeverson
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Abr 22, 2018 00:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por Gebe » Dom Abr 22, 2018 17:11
por Gebe » Dom Abr 22, 2018 17:11
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada de função de duas variáveis] Dúvida numa passagem
por Fabio Wanderley » Sáb Dez 06, 2014 14:51
- 4 Respostas
- 3268 Exibições
- Última mensagem por adauto martins

Qua Dez 10, 2014 21:28
Cálculo: Limites, Derivadas e Integrais
-
- Derivada com várias variáveis
por kryzay » Seg Mai 14, 2012 09:23
- 2 Respostas
- 2173 Exibições
- Última mensagem por kryzay

Seg Mai 14, 2012 10:58
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada com várias variáveis
por Fernandobertolaccini » Sex Dez 19, 2014 17:28
- 1 Respostas
- 1968 Exibições
- Última mensagem por adauto martins

Qui Dez 25, 2014 13:09
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada com várias variáveis
por Fernandobertolaccini » Sex Dez 19, 2014 17:33
- 1 Respostas
- 1708 Exibições
- Última mensagem por adauto martins

Ter Dez 23, 2014 16:28
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada com várias variáveis
por Fernandobertolaccini » Sex Dez 19, 2014 17:44
- 2 Respostas
- 2045 Exibições
- Última mensagem por adauto martins

Qua Dez 24, 2014 11:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 48 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
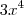 – 2xy² +
– 2xy² + 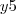

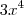 – 2xy² +
– 2xy² + 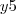

– 2xy² +
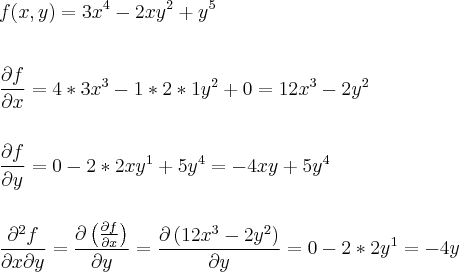
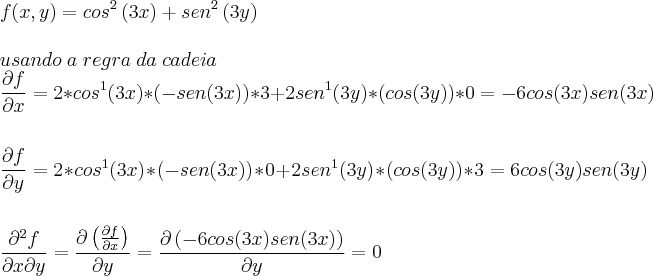
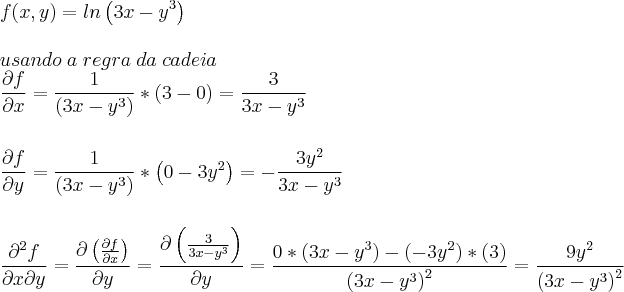



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.