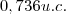![y= \frac{3 \sqrt[]{x}}{2} y= \frac{3 \sqrt[]{x}}{2}](/latexrender/pictures/c2e16ceef443660893bbca5d2b3a0978.png) com
com 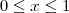 .
.Fui fazendo o cálculo, achei a derivada de
 , até que cheguei nessa equação:
, até que cheguei nessa equação: ![L=\int_{0}^{1}\sqrt[]{1+\frac{9}{16x}} dx L=\int_{0}^{1}\sqrt[]{1+\frac{9}{16x}} dx](/latexrender/pictures/203994dc43579a4c77b39889d51c3911.png) , e, depois disso, não consegui fazer mais nada. Tentei até o método de substituição, substituindo o radicando por
, e, depois disso, não consegui fazer mais nada. Tentei até o método de substituição, substituindo o radicando por  , mas o resultado do
, mas o resultado do 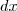 deu
deu 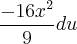 , não sei como tirar esse
, não sei como tirar esse  da integral. Gostaria que alguém pudesse me auxiliar a sair dessa integração.
da integral. Gostaria que alguém pudesse me auxiliar a sair dessa integração.A resposta do gabarito é:
![\frac{8}{27}*\sqrt[]{{\left(\frac{13}{4}\right)}}^{3}-1 u.c. \frac{8}{27}*\sqrt[]{{\left(\frac{13}{4}\right)}}^{3}-1 u.c.](/latexrender/pictures/316438120cf94149b3c28edd7c158b43.png) ou aproximadamente
ou aproximadamente