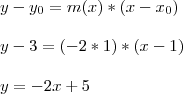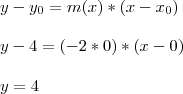-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480827 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 543221 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 506962 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 737483 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2185423 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por ton_cineasta » Qui Abr 05, 2018 18:26
por ton_cineasta » Qui Abr 05, 2018 18:26
Determine a equação da reta tangente ao gráfico da função a seguir nos pontos dados e trace o gráficos:
f(x) = -x² - 4 nos pontos P(1,3) e Q(0,4)
Achei o m(x) = lim -2x , mas não tô conseguindo traçar as retas no gráfico. Se fosse, por exemplo, em (X1 = 0), eu saberia.
/\x->0
Mas com esses pontos dados não sei como aplicar na fórmula y - f(X)= [m(X)][X - X1].
Obrigado!
-
ton_cineasta
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 05, 2018 18:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Jogos Digitais
- Andamento: cursando
 por Gebe » Sex Abr 06, 2018 05:58
por Gebe » Sex Abr 06, 2018 05:58
Não sei da onde tu tirou esse
limite, só precisa tirar a derivada, veja:
1) Derivada da função pra achar m(x):

2) Equação da reta no ponto (1,3):
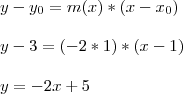
Agora só achar outro ponto da reta e traçar (ex.: pra x=0 -> y=5)
3) Equação da rata no ponto (0,4):
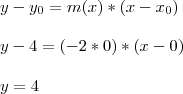
Como se esperava a tg é 0 no vertice da função, ou seja, será uma reta constante em y=4
Espero ter ajudado, bons estudos.
-
Gebe
- Colaborador Voluntário

-
- Mensagens: 158
- Registrado em: Qua Jun 03, 2015 22:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
 por ton_cineasta » Seg Abr 09, 2018 15:47
por ton_cineasta » Seg Abr 09, 2018 15:47
Muito obrigado! Ajudou sim!!!
Ainda tô me embananando porque as retas não ficaram tangentes à curva do gráfico da função. Mas deve ser algum detalhe que eu tô deixando passar...
-
ton_cineasta
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 05, 2018 18:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Jogos Digitais
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada reta tangente ao gráfico
por Carolminera » Dom Jul 06, 2014 16:53
- 1 Respostas
- 2266 Exibições
- Última mensagem por e8group

Dom Jul 06, 2014 20:11
Cálculo: Limites, Derivadas e Integrais
-
- Derivada reta tangente ao gráfico
por Carolminera » Qua Jul 23, 2014 11:33
- 1 Respostas
- 1537 Exibições
- Última mensagem por Russman

Qua Jul 23, 2014 21:08
Cálculo: Limites, Derivadas e Integrais
-
- A reta tangente ao gráfico da função (derivadas)
por Ana Maria da Silva » Dom Jun 09, 2013 21:43
- 2 Respostas
- 1791 Exibições
- Última mensagem por Ana Maria da Silva

Qua Jun 12, 2013 20:27
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] Reta tangente e Reta perpendicular
por antonelli2006 » Ter Nov 22, 2011 11:21
- 1 Respostas
- 8349 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 14:28
Cálculo: Limites, Derivadas e Integrais
-
- [Reta Paralela à Reta Tangente]
por raimundoocjr » Qui Mai 30, 2013 18:44
- 0 Respostas
- 1007 Exibições
- Última mensagem por raimundoocjr

Qui Mai 30, 2013 18:44
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.