Esta é uma questão um tanto difícil de ser resolvida.
Vamos partir do fato que, derivando implicitamente a equação, teremos como declividade:
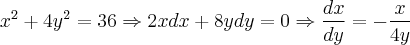
Agora, vamos isolar
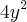
![4{y}^{2} = 36 - {x}^{2} \: \: \: [1] 4{y}^{2} = 36 - {x}^{2} \: \: \: [1]](/latexrender/pictures/e55e6de38d17c0b6d2f8b8454b535a2c.png)
A Equação da reta em qualquer ponto da elipse deverá ser:
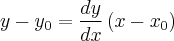
Sabemos um ponto desta reta (12, 3). Utilizando este ponto na equação acima, teremos:
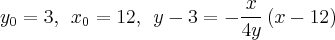
Resolvendo:
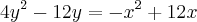
Usando o fato [1] acima nesta última equação, tem-se que:
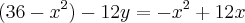
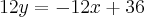
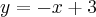
Substituindo-se este resultado para y em nossa equação original do problema, obtem-se:
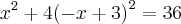
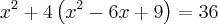
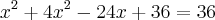
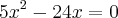

Dessa maneira,
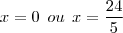
O que é esperado.
Logo, y, tomando-se x = 0, deverá ser y = 3. Ponto (0, 3). E para x = 24/5, e como:
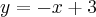
então, y deverá ser:
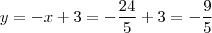
Assim, agora podemos obter finalmente o que nos foi solicitado, ou seja, as equações das retas tangentes que passam pelo ponto (12, 3).
Para a primeira reta que passa pela elipse tocando em (0, 3) teremos:
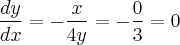
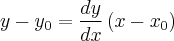
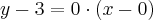

que é a equação da primeira reta que passa no ponto (0,3) e também pelo ponto (12,3).
Utilizando (24/5, -9/5), a declividade serã de:

e a reta que passa por este ponto (24/5, -9/5) e também pelo ponto (12, 3) deverá ser:

Assim, a segunta equação de reta será

O método que utilizei é um tanto longa e trabalhosa. Pode ser que existam meios mais rápidos e eficientes de se resolver este problema, porém isto é o que me veio em mente. Espero ter ajudado.
Se desejar ver o grafico e essas tangentes, acesse
http://simples.zapto.org/?p=675Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali



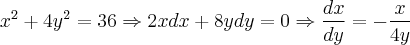
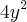
![4{y}^{2} = 36 - {x}^{2} \: \: \: [1] 4{y}^{2} = 36 - {x}^{2} \: \: \: [1]](/latexrender/pictures/e55e6de38d17c0b6d2f8b8454b535a2c.png)
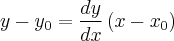
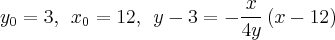
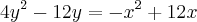
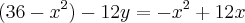
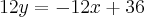
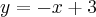
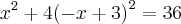
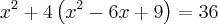
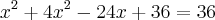
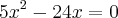

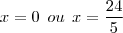
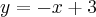
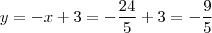
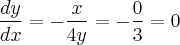
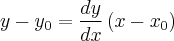
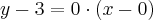





![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.