-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478868 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 536348 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 500019 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 718859 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2144608 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por mataprendizagem » Dom Ago 20, 2017 20:13
por mataprendizagem » Dom Ago 20, 2017 20:13
Boa noite galera, tentei fazer o exercicio de 4 jeitos diferentes mas nao deu certo . Alguem sabe?
para an-1 sendo an>= 2 calculei a2-1 = 1 então an=1+(-1)^²=2 e sucessivamente para 6 primeiros termos. Adotei 1 para an-1 em todos os termos da série zerando todos com expoente ímpar mas não estou certo disso.
- Anexos
-

-
mataprendizagem
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Ago 20, 2017 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia
- Andamento: cursando
 por DanielFerreira » Sex Ago 25, 2017 22:36
por DanielFerreira » Sex Ago 25, 2017 22:36
Olá! seja bem-vindo(a)!!
Atente para o fato de
n ser maior ou igual a dois. Assim, o que temos a fazer é determinar os seis termos substituindo...
Primeiro termo: a_2

Segundo termo: a_3
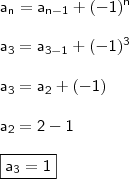
Terceiro termo: a_4
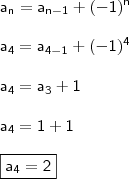
Agora é com você. Encontre
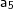
,

,

e efetue a soma dos termos.
Feito isto, diga quanto encontrou como resposta, ok?!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites - Questão fácil?
por iceman » Dom Set 16, 2012 19:10
- 1 Respostas
- 1281 Exibições
- Última mensagem por DanielFerreira

Dom Set 16, 2012 19:20
Cálculo: Limites, Derivadas e Integrais
-
- dúvida fácil
por TAE » Ter Mai 22, 2012 21:04
- 3 Respostas
- 1740 Exibições
- Última mensagem por DanielFerreira

Qui Mai 24, 2012 11:04
Álgebra Elementar
-
- [Limites] Dúvida sobre limites laterais
por Subnik » Sáb Abr 04, 2015 18:24
- 1 Respostas
- 2387 Exibições
- Última mensagem por DanielFerreira

Dom Abr 12, 2015 16:10
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITES] Dúvida em questão de Limites no infinito
 por Jacques » Ter Jul 12, 2016 21:42
por Jacques » Ter Jul 12, 2016 21:42
- 4 Respostas
- 6865 Exibições
- Última mensagem por vitor_jo

Qua Jul 13, 2016 16:51
Cálculo: Limites, Derivadas e Integrais
-
- DUVIDA LIMITES
 por paulovlg » Qua Jun 18, 2014 23:21
por paulovlg » Qua Jun 18, 2014 23:21
- 1 Respostas
- 1547 Exibições
- Última mensagem por e8group

Qui Jun 19, 2014 14:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 116 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



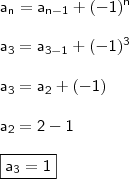
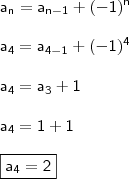
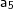 ,
,  ,
,  e efetue a soma dos termos.
e efetue a soma dos termos.