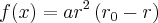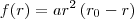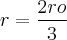-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478828 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 535905 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 499561 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 717547 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2142385 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por fcosta » Ter Nov 29, 2016 12:32
por fcosta » Ter Nov 29, 2016 12:32
Boa tarde!
Alguém por favor pode me dizer como derivo isso:
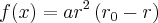
-
fcosta
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Nov 29, 2016 12:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: tecnologia em automação
- Andamento: cursando
 por Cleyson007 » Qua Nov 30, 2016 09:23
por Cleyson007 » Qua Nov 30, 2016 09:23
fcosta escreveu: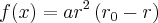
Isso não é uma função de x. O correto é:
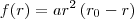
Para derivar esta função utilize a Regra do Produto.
f' (r) = 2ar (r
o - r) + (-1)(ar²) = 2arr
o - 3ar²
Repare que como estou derivando em função de "r" o r
o é constante, logo, sua
derivada é zero.
Sou professor de Matemática e tenho um trabalho muito bacana destinado a ajudar alunos que possuem muita dificuldade. Caso tenha interesse deixo o meu contato via WhatsApp (38) 99889-5755.
Estou com um pacote promocional de video-aula via Skype.
Qualquer dúvida estou a disposição.
Abraço,
Prof. Clésio
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por fcosta » Qua Nov 30, 2016 13:35
por fcosta » Qua Nov 30, 2016 13:35
Olá, professor!
Então eu continuei e cheguei ao máximo de
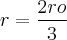
Está certo?
-
fcosta
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Nov 29, 2016 12:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: tecnologia em automação
- Andamento: cursando
 por Cleyson007 » Qua Nov 30, 2016 17:34
por Cleyson007 » Qua Nov 30, 2016 17:34
Exatamente

O máximo ocorre quando f ' = 0 (
Derivada da função f é igual a zero).
Pensou na proposta que lhe apresentei?
Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1227
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por fcosta » Qua Nov 30, 2016 18:54
por fcosta » Qua Nov 30, 2016 18:54
Sim pensei...
Logo entro em contato!
Obrigado
-
fcosta
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Nov 29, 2016 12:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: tecnologia em automação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- DERIVAR ou INTEGRAR
por DESESPERADO » Qui Nov 11, 2010 14:14
- 15 Respostas
- 12133 Exibições
- Última mensagem por andrefahl

Sex Nov 12, 2010 17:45
Cálculo: Limites, Derivadas e Integrais
-
- Derivar e simplificar
por Jota17 » Sáb Nov 05, 2011 22:40
- 1 Respostas
- 1186 Exibições
- Última mensagem por LuizAquino

Ter Nov 08, 2011 00:22
Cálculo: Limites, Derivadas e Integrais
-
- derivar a função
por SILMARAKNETSCH » Qua Nov 14, 2012 18:21
- 3 Respostas
- 3416 Exibições
- Última mensagem por SILMARAKNETSCH

Qua Nov 14, 2012 21:57
Funções
-
- Derivar f(X) = (x²+7)²Raiz(1-x)
por Henrique Webber » Sex Nov 22, 2013 20:02
- 0 Respostas
- 915 Exibições
- Última mensagem por Henrique Webber

Sex Nov 22, 2013 20:02
Cálculo: Limites, Derivadas e Integrais
-
- Derivar uma função
por rcs01 » Qui Abr 30, 2015 09:48
- 0 Respostas
- 1990 Exibições
- Última mensagem por rcs01

Qui Abr 30, 2015 09:48
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 123 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.