-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478130 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 531494 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495037 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 704808 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2119874 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por adauto martins » Qui Dez 01, 2016 11:11
por adauto martins » Qui Dez 01, 2016 11:11
tomemos a velocidade da trajetoria em algum plano
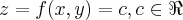
,q.sera dada por:
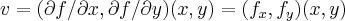
,onde
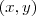
um ponto qquer da trajetoria do plano
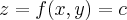
...queremos a componente perpendicular em z,com relaçao ao vetor velocidade no ponto (2,-3),ou seja
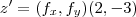
...logo:
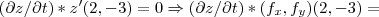
![(\partial z/ \partial t)*(-2x/\sqrt[]{(49-{x}^{2}-{y}^{2}}),-2y/\sqrt[]{(49-{x}^{2}-{y}^{2}})(2,-3)=0 (\partial z/ \partial t)*(-2x/\sqrt[]{(49-{x}^{2}-{y}^{2}}),-2y/\sqrt[]{(49-{x}^{2}-{y}^{2}})(2,-3)=0](/latexrender/pictures/6f5ea8a4db394b832df529c9df3c44db.png)
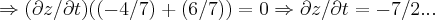
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Dez 01, 2016 16:42
por adauto martins » Qui Dez 01, 2016 16:42
a resoluçao dessa questao esta incorreta,logo q. a resolver postarei...obrigado
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sáb Dez 03, 2016 13:25
por adauto martins » Sáb Dez 03, 2016 13:25
primeiramente a pergunta da questao esta mal formulada...o que o autor pede esta calculado acima,como fiz e seria:
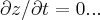
,onde meu erro foi na
derivada,ao qual é:
![f'(x,y)=(-x/\sqrt[]{49-{x}^{2}-{y}^{2}},-y/\sqrt[]{49-{x}^{2}-{y}^{2}}) f'(x,y)=(-x/\sqrt[]{49-{x}^{2}-{y}^{2}},-y/\sqrt[]{49-{x}^{2}-{y}^{2}})](/latexrender/pictures/2e90d93fc4dc1e277bb7813f930709a6.png)
,no ponto (2,-3),seria:
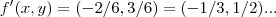
...bom,talvez o autor pede o versor normal á tangente(velocidade)...ai o calculo seria:
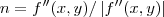
,q. mede a aceleraçao centrifuga(ou centripeta,caso com sinal negativo) do ponto na curva...que é o que geralmente costuma-se se pedir...bom,é isso é o que eu pude analisar...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Regra da poligonal e Regra do Paralelogramo
 por fernando7 » Qui Abr 12, 2018 22:22
por fernando7 » Qui Abr 12, 2018 22:22
- 1 Respostas
- 3803 Exibições
- Última mensagem por Gebe

Sex Abr 13, 2018 00:49
Álgebra Linear
-
- Regra de 3
por Roberta » Ter Jul 14, 2009 22:19
- 4 Respostas
- 9438 Exibições
- Última mensagem por Engligen

Sáb Jul 09, 2016 03:04
Desafios Enviados
-
- Regra de 3
por Raphael Feitas10 » Ter Mai 24, 2011 02:31
- 2 Respostas
- 2779 Exibições
- Última mensagem por Raphael Feitas10

Qui Mai 26, 2011 01:56
Sistemas de Equações
-
- Regra de 3
por Raphael Feitas10 » Qua Jul 20, 2011 00:45
- 2 Respostas
- 1633 Exibições
- Última mensagem por Raphael Feitas10

Sex Jul 22, 2011 13:59
Sistemas de Equações
-
- Regra de 3
por Raphael Feitas10 » Dom Dez 18, 2011 12:46
- 3 Respostas
- 3121 Exibições
- Última mensagem por Raphael Feitas10

Qua Dez 21, 2011 01:42
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 53 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



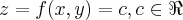 ,q.sera dada por:
,q.sera dada por: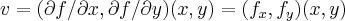 ,onde
,onde 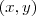 um ponto qquer da trajetoria do plano
um ponto qquer da trajetoria do plano 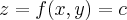 ...queremos a componente perpendicular em z,com relaçao ao vetor velocidade no ponto (2,-3),ou seja
...queremos a componente perpendicular em z,com relaçao ao vetor velocidade no ponto (2,-3),ou seja 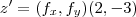 ...logo:
...logo: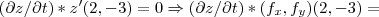
![(\partial z/ \partial t)*(-2x/\sqrt[]{(49-{x}^{2}-{y}^{2}}),-2y/\sqrt[]{(49-{x}^{2}-{y}^{2}})(2,-3)=0 (\partial z/ \partial t)*(-2x/\sqrt[]{(49-{x}^{2}-{y}^{2}}),-2y/\sqrt[]{(49-{x}^{2}-{y}^{2}})(2,-3)=0](/latexrender/pictures/6f5ea8a4db394b832df529c9df3c44db.png)
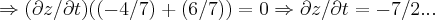


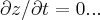 ,onde meu erro foi na derivada,ao qual é:
,onde meu erro foi na derivada,ao qual é:![f'(x,y)=(-x/\sqrt[]{49-{x}^{2}-{y}^{2}},-y/\sqrt[]{49-{x}^{2}-{y}^{2}}) f'(x,y)=(-x/\sqrt[]{49-{x}^{2}-{y}^{2}},-y/\sqrt[]{49-{x}^{2}-{y}^{2}})](/latexrender/pictures/2e90d93fc4dc1e277bb7813f930709a6.png) ,no ponto (2,-3),seria:
,no ponto (2,-3),seria: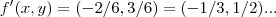 ...bom,talvez o autor pede o versor normal á tangente(velocidade)...ai o calculo seria:
...bom,talvez o autor pede o versor normal á tangente(velocidade)...ai o calculo seria: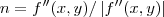 ,q. mede a aceleraçao centrifuga(ou centripeta,caso com sinal negativo) do ponto na curva...que é o que geralmente costuma-se se pedir...bom,é isso é o que eu pude analisar...
,q. mede a aceleraçao centrifuga(ou centripeta,caso com sinal negativo) do ponto na curva...que é o que geralmente costuma-se se pedir...bom,é isso é o que eu pude analisar...
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
