-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478253 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 532697 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 496211 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 708325 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2126085 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Fred Pellegrini » Sex Out 28, 2016 18:21
por Fred Pellegrini » Sex Out 28, 2016 18:21
Como provar os seguintes limites pela definição?
a) Lim (x² - 2x + 1) = 1
x->2
b) lim (x² + 4x + 4) = 1
x->-1
c) lim (3x² - 7x +2) = -2
x->1
-
Fred Pellegrini
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Out 28, 2016 18:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por adauto martins » Seg Out 31, 2016 10:14
por adauto martins » Seg Out 31, 2016 10:14
essa questao eu ja resolvi ela uma pa de vezes,mas vamos a mais uma:
definiçao formal de limite:
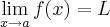
dado um
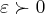
,existe pelo menos um
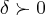
(existem ifinitos deltas,por que?),tal que satisfaça a:
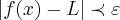
...entao vamos a questao a),as outras ficam como exercicios...

:
entao dado um
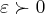
,existe pelo um
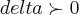
,
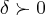
...esse

tera q. ser em funçao do

dado,ou seja:
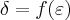
e geralmente,escolhe-se o menor

,ou seja
![\delta =min[{\delta}_{1},{\delta}_{2},...] \delta =min[{\delta}_{1},{\delta}_{2},...]](/latexrender/pictures/d4247bbef86a62e625a9a6c176f73ffc.png)
...agora vamos ao calculo...temos q.
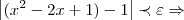
e q.
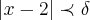
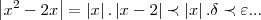
,como
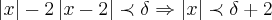
,logo temos q.
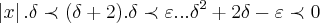
...resolvendo essa inequaçao,encontraremos dois deltas...
![{\delta}_{1}=\sqrt[]{1+\varepsilon}-1,{\delta}_{2}=\sqrt[]{1+\varepsilon}+1... {\delta}_{1}=\sqrt[]{1+\varepsilon}-1,{\delta}_{2}=\sqrt[]{1+\varepsilon}+1...](/latexrender/pictures/3ab1e8b9e36a928ae2654c9f0fc5400a.png)
...vamos tomar
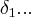
...logo,teremos:
![\left|({x}^{2}-2x+1)-1 \right|=\left|{x}^{2}-2x \right|\preceq\left|x \right|.\left|x-2 \right|\prec (\delta+2).\delta={\delta}^{2}+2.\delta={(\sqrt[]{\varepsilon+1}-1})^{2}+2.(\sqrt[]{\varepsilon+1})=...\prec \varepsilon \left|({x}^{2}-2x+1)-1 \right|=\left|{x}^{2}-2x \right|\preceq\left|x \right|.\left|x-2 \right|\prec (\delta+2).\delta={\delta}^{2}+2.\delta={(\sqrt[]{\varepsilon+1}-1})^{2}+2.(\sqrt[]{\varepsilon+1})=...\prec \varepsilon](/latexrender/pictures/244cca570e64f5ff9db7f6639bd3d9fb.png)
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Limites pela definição formal
por joaofonseca » Ter Out 11, 2011 09:38
- 1 Respostas
- 2430 Exibições
- Última mensagem por joaofonseca

Qua Out 12, 2011 19:29
Cálculo: Limites, Derivadas e Integrais
-
- Limites pela definição formal
por ramoncampos » Ter Nov 01, 2016 21:20
- 4 Respostas
- 8719 Exibições
- Última mensagem por ramoncampos

Sex Nov 04, 2016 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Limites pela definiçao
 por JoaoLuiz07 » Qui Ago 27, 2015 16:55
por JoaoLuiz07 » Qui Ago 27, 2015 16:55
- 1 Respostas
- 1534 Exibições
- Última mensagem por adauto martins

Sáb Ago 29, 2015 20:52
Cálculo: Limites, Derivadas e Integrais
-
- Derivada pela Definiçao
por PeIdInHu » Sáb Mai 22, 2010 17:24
- 1 Respostas
- 1909 Exibições
- Última mensagem por admin

Sáb Mai 22, 2010 18:24
Cálculo: Limites, Derivadas e Integrais
-
- Integral pela definição
por ARCS » Sáb Abr 09, 2011 15:49
- 1 Respostas
- 1344 Exibições
- Última mensagem por LuizAquino

Dom Abr 10, 2011 13:33
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 92 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



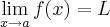
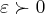 ,existe pelo menos um
,existe pelo menos um 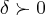 (existem ifinitos deltas,por que?),tal que satisfaça a:
(existem ifinitos deltas,por que?),tal que satisfaça a: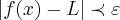 ...entao vamos a questao a),as outras ficam como exercicios...
...entao vamos a questao a),as outras ficam como exercicios... :
: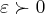 ,existe pelo um
,existe pelo um 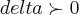 ,
,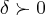 ...esse
...esse  tera q. ser em funçao do
tera q. ser em funçao do  dado,ou seja:
dado,ou seja: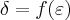 e geralmente,escolhe-se o menor
e geralmente,escolhe-se o menor  ,ou seja
,ou seja ![\delta =min[{\delta}_{1},{\delta}_{2},...] \delta =min[{\delta}_{1},{\delta}_{2},...]](/latexrender/pictures/d4247bbef86a62e625a9a6c176f73ffc.png) ...agora vamos ao calculo...temos q.
...agora vamos ao calculo...temos q.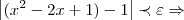 e q.
e q.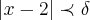
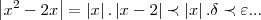 ,como
,como 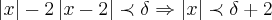 ,logo temos q.
,logo temos q.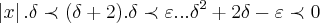 ...resolvendo essa inequaçao,encontraremos dois deltas...
...resolvendo essa inequaçao,encontraremos dois deltas...![{\delta}_{1}=\sqrt[]{1+\varepsilon}-1,{\delta}_{2}=\sqrt[]{1+\varepsilon}+1... {\delta}_{1}=\sqrt[]{1+\varepsilon}-1,{\delta}_{2}=\sqrt[]{1+\varepsilon}+1...](/latexrender/pictures/3ab1e8b9e36a928ae2654c9f0fc5400a.png) ...vamos tomar
...vamos tomar 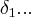 ...logo,teremos:
...logo,teremos:![\left|({x}^{2}-2x+1)-1 \right|=\left|{x}^{2}-2x \right|\preceq\left|x \right|.\left|x-2 \right|\prec (\delta+2).\delta={\delta}^{2}+2.\delta={(\sqrt[]{\varepsilon+1}-1})^{2}+2.(\sqrt[]{\varepsilon+1})=...\prec \varepsilon \left|({x}^{2}-2x+1)-1 \right|=\left|{x}^{2}-2x \right|\preceq\left|x \right|.\left|x-2 \right|\prec (\delta+2).\delta={\delta}^{2}+2.\delta={(\sqrt[]{\varepsilon+1}-1})^{2}+2.(\sqrt[]{\varepsilon+1})=...\prec \varepsilon](/latexrender/pictures/244cca570e64f5ff9db7f6639bd3d9fb.png) ...
...





