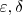,que:
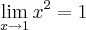...soluçao:
da definiçao,teremos que:
dado um
,existe pelo menos um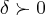 
tal que:
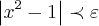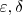... sao tais que:
,sempre:entao escolhemos um
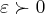,e vamos a procura de pelo menos um 
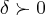(existem infinitos,por que?)que satisfaça a igualdade 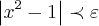...teremos entao que:
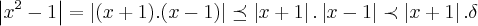...agora é usar as desiqualdades triangulares e encontrar esse 
...temos q.:
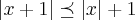...como o limite esta sendo calculado nas proximidades de 1,podemos tomar 
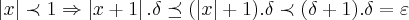,ou ainda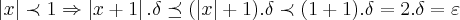 
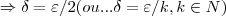e etc...geralmente escolhemos o menor possivel,o qual sera o supremo do intervalo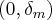
,onde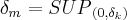 
,mas tambem podemos tomar qquer 
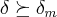,que satisfaça 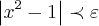...vamos encontrar um ,apartir da algebra das desiqualdades:temos q.:
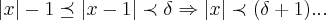,teremos entao q:
,logo ![{\delta}^{2}+2\delta -\varepsilon=0\Rightarrow \delta=-1-\sqrt[]{(1+\varepsilon)}(esse nao serve)...\delta=-1+\sqrt[]{(1+\varepsilon)}](/latexrender/pictures/df5f010737d675b5fb5a8b50be6f29ed.png "{\delta}^{2}+2\delta -\varepsilon=0\Rightarrow \delta=-1-\sqrt[]{(1+\varepsilon)}(esse nao serve)...\delta=-1+\sqrt[]{(1+\varepsilon)}")
...entao: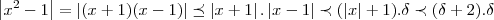
![\prec {(-1+\sqrt[]{(1+\varepsilon})}^{2}+2(-1+\sqrt[]{(1+\varepsilon)}=\varepsilon...](/latexrender/pictures/2c39d98c8643d270cefcb58603435475.png "\prec {(-1+\sqrt[]{(1+\varepsilon})}^{2}+2(-1+\sqrt[]{(1+\varepsilon)}=\varepsilon...")
por 
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.