 por LuisLemos » Seg Ago 01, 2016 22:36
por LuisLemos » Seg Ago 01, 2016 22:36
-
LuisLemos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jul 27, 2016 21:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Graduando de engenharia mecânica
- Andamento: cursando
 por Cleyson007 » Ter Ago 02, 2016 12:40
por Cleyson007 » Ter Ago 02, 2016 12:40
Olá, bom dia amigo!
O polinômio de Taylor de ordem 2 de f(x) ao redor de p é dado por:
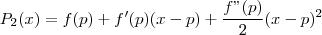
Comente qualquer dúvida.
Caso queira conhecer melhor o nosso trabalho, acesse:
viewtopic.php?f=151&t=13614Abraço,
Prof. Clésio
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- polinomio de taylor
por ezidia51 » Ter Set 24, 2019 00:09
- 6 Respostas
- 6044 Exibições
- Última mensagem por ezidia51

Qua Set 25, 2019 23:49
Cálculo: Limites, Derivadas e Integrais
-
- Polinômio de Taylor de ordem 2
por Maisa_Rany » Seg Nov 19, 2018 16:53
- 2 Respostas
- 8115 Exibições
- Última mensagem por Maisa_Rany

Ter Nov 20, 2018 16:26
Cálculo: Limites, Derivadas e Integrais
-
- [polinômio de taylor] - dúvida em exercício
 por natanaelskt » Dom Jun 29, 2014 13:02
por natanaelskt » Dom Jun 29, 2014 13:02
- 2 Respostas
- 2804 Exibições
- Última mensagem por natanaelskt

Qua Jul 02, 2014 02:08
Cálculo: Limites, Derivadas e Integrais
-
- Polinomio de taylor - Dúvida sobre o erro.
por natanaelskt » Seg Jun 23, 2014 18:55
- 0 Respostas
- 1671 Exibições
- Última mensagem por natanaelskt

Seg Jun 23, 2014 18:55
Cálculo: Limites, Derivadas e Integrais
-
- [polinômio de taylor] - Dúvida sobre o exercício
 por natanaelskt » Ter Jul 08, 2014 11:41
por natanaelskt » Ter Jul 08, 2014 11:41
- 0 Respostas
- 1725 Exibições
- Última mensagem por natanaelskt

Ter Jul 08, 2014 11:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é
é 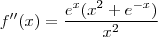 , e sabendo que f(1) = 1,
, e sabendo que f(1) = 1, 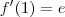 ,
, por um polinômio de grau 2 em torno de x = 1.
por um polinômio de grau 2 em torno de x = 1. .
.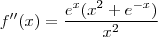 ,
,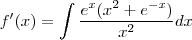
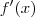 =
= 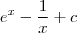
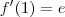
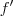 (1) =
(1) = 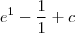 = e
= e
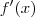 =
= 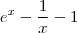
 :
: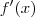 =
= 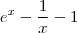 ,
,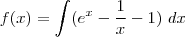

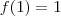

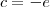
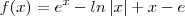


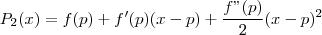


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.