-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 477880 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 529556 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 493102 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 699178 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2109726 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por LuisLemos » Qua Jul 27, 2016 21:27
por LuisLemos » Qua Jul 27, 2016 21:27
Boa noite, não estou conseguindo entender como encontrar o máximo e o minimo global de uma função, após ter encontrado o máximo e o minimo local. Como exemplo, estou colocando uma questão que tentei resolver:
Determine os pontos de máximo e mínimo locais da função 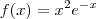 , dizendo quais destes pontos são máximos ou mínimos globais.
, dizendo quais destes pontos são máximos ou mínimos globais.O que eu fiz para encontrar os pontos de mínimo locais:
1º - Derivei a função: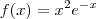
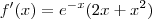
2º - Igualei a função a zero para encontrar os pontos críticos: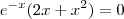
Como

é sempre positivo, a função só poderá ser zero quando
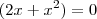
. Portanto as raízes dessa expressão (-2 e 0) serão os pontos críticos.
3º - Calculei a f'(x) para -3 , -1 e 1 para saber se a função é crescente ou decrescente antes e depois dos pontos críticos.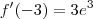
(positivo)
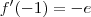
(negativo)
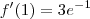
(positivo)
4º - Determinei os pontos de mínimo e máximo locais:Como a função é crescente antes de -2 e decrescente após o -2, logo ele é um ponto de máximo local.
E como a função é decrescente antes do 0 e crescente após 0 , ele é um ponto de mínimo local.
A partir de agora eu não sei o que devo fazer para encontrar os pontos de máximo e mínimo globais, caso existam.
Obs: O gabarito da questão informa que a função não possui máximo global e que o ponto 0 é mínimo global.
-
LuisLemos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jul 27, 2016 21:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Graduando de engenharia mecânica
- Andamento: cursando
 por Daniel Bosi » Qua Jul 27, 2016 23:21
por Daniel Bosi » Qua Jul 27, 2016 23:21
Olá LuisLemos.
Primeiramente, muito obrigado por ter postado a sua resolução de forma completa.

Você cometeu um erro de sinal no momento de derivar. Perceba que quando derivamos

pela regra
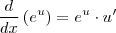
obtemos
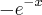
.
Assim, derivando
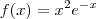
pela regra do produto:
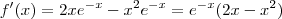
Assim, as raízes de
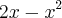
são 0 e 2.
Substituindo -1, 1 e 3 na
derivada:
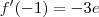
(negativo, portanto decrescente)
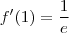
(positivo, portanto crescente)

(negativo, portanto decrescente)
OBS.: Essa parte
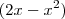
da
derivada da função original que usamos para encontrar os pontos críticos é uma parábola. Nos intervalos onde esta parábola tem imagem negativa, a função original é decrescente. No intervalo onde esta parábola tem imagem positiva, a função original é crescente. O

que multiplica
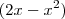
na
derivada não muda os pontos críticos nem o sinal da imagem, embora mude a função. Mas uma vez que o que nos interessa é analisar os pontos críticos e o sinal da imagem, convém considerar apenas a parte
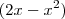
por ser mais simples.
A partir dessa análise você já pode ter uma ideia de que 0 é um mínimo e 2 é um máximo. Como saber se eles são locais ou globais?
Para responder a essa questão eu aconselho fazer uma avaliação da função original
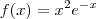
.
Essa função claramente não pode assumir valores negativos (pois nem

nem

podem ser negativos, independe do x; você consegue ver isso intuitivamente?), então é razoável dizer que a função
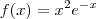
não pode ter imagem negativa. Se ela não pode ter imagem negativa, claramente 0 é um mínimo global.
Em relação ao ponto máximo 2, basta substituir um dos pontos usados para teste, -1 por exemplo, na função original
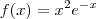
e perceber que o ponto -1 na função original dá a constante neperiana

, que é maior que 2. Portanto, 2 é máximo local.
Plotei a função original
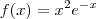
(em verde) e a função
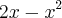
(em azul) no GeoGebra para você visualizar como todos esses pontos das funções se relacionam. Perceba como o gráfico verde muda a tendência de crescimento e decrescimento nas raízes da parábola azul (isto é, quando a imagem y da parábola muda de negativo para positivo e vice e versa).

Qualquer dúvida volte a questionar.
-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuisLemos » Qui Jul 28, 2016 00:20
por LuisLemos » Qui Jul 28, 2016 00:20
Nossa, obrigado pela resposta.
De fato eu errei o sinal na hora de derivar.
Pelo gráfico que você colocou eu consegui visualisar a relação entre a função não possuir imagem negativa com o zero ser mínimo global. Pois se a função não atinge valores menores que zero, ele será o menor valor da função. Sendo assim o mínimo global.
Em relação ao 2 ser somente máximo local. Você pegou um dos pontos utilizados para determinar os máximos e mínimos locais e substituiu na função original. Como o valor obtido foi maior que 2, então o 2 não poderia ser máximo global.
Em relação a isso eu fiquei com uma dúvida. Digamos que eu tenha uma outra função e que essa função possua vários pontos críticos. Eu teria que substituir vários pontos na função original para ter certeza que nenhum deles é superior ao ponto que eu encontrei como máximo local? ou teria uma forma mais prática de resolver?
-
LuisLemos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jul 27, 2016 21:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Graduando de engenharia mecânica
- Andamento: cursando
 por Daniel Bosi » Qui Jul 28, 2016 00:43
por Daniel Bosi » Qui Jul 28, 2016 00:43
Vou pegar o caso desse exercício como base para responder a sua questão, e a partir disso podemos generalizar a ideia.
A partir da
derivada e da análise dos pontos críticos, percebemos que a função decresce antes do zero, cresce no intervalo aberto de 0 a 2, e volta a decrescer após o 2.
Percebemos também que esta função não pode ter imagem negativa.
Se ela não pode ter imagem negativa e descobrimos que o 0 é mínimo global, sabemos que essa função tem 0 como elemento mínimo.
Sabemos que ela tem um mínimo. Mas será que ela tem um máximo?
Recapitulando, tudo que sabemos a partir dos pontos críticos e do sinal da
derivada é que: ela decresce até o zero, cresce de 0 a 2, decresce a partir do 2.
O pulo do gato consiste em perceber que: se ela decresce até o 0 sem um ponto crítico nos números negativos, existe uma chance grande de haver valores maiores que o 2 antes do 0.
Se não há ponto crítico antes desse decrescimento, isso dá uma boa intuição que a função cresce sem limite quando x vai a

.
A estratégia é sempre testar valores que estão além dos pontos críticos "de fora", além de pensar sobre o comportamento geral da função.
Em caso de dúvidas estamos aí.

-
Daniel Bosi
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Mai 16, 2016 21:37
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por LuisLemos » Qui Jul 28, 2016 00:49
por LuisLemos » Qui Jul 28, 2016 00:49
Nossa, depois de várias video aulas você me fez entender isso finalmente.
Muito obrigado


-
LuisLemos
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jul 27, 2016 21:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Graduando de engenharia mecânica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo (Maximos e Minimos)]
 por moraes1321 » Sáb Dez 01, 2012 10:49
por moraes1321 » Sáb Dez 01, 2012 10:49
- 2 Respostas
- 2887 Exibições
- Última mensagem por moraes1321

Ter Dez 04, 2012 22:10
Cálculo: Limites, Derivadas e Integrais
-
- Calculo Maximos e Minimos
por brunnoguilherme » Dom Jan 13, 2013 19:58
- 0 Respostas
- 1277 Exibições
- Última mensagem por brunnoguilherme

Dom Jan 13, 2013 19:58
Cálculo: Limites, Derivadas e Integrais
-
- Calculo III - Máximos e Minimos
por lukeibol » Seg Mai 08, 2017 14:47
- 0 Respostas
- 1070 Exibições
- Última mensagem por lukeibol

Seg Mai 08, 2017 14:47
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo I] Exercício - Máximos e Mínimos
por Pessoa Estranha » Dom Nov 16, 2014 11:43
- 3 Respostas
- 2151 Exibições
- Última mensagem por felipederaldino

Qui Nov 27, 2014 11:28
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo I] Exercício - Máximos e Mínimos
por Pessoa Estranha » Dom Nov 16, 2014 16:53
- 0 Respostas
- 1665 Exibições
- Última mensagem por Pessoa Estranha

Dom Nov 16, 2014 16:53
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 29 visitantes
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?

O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois

2°) Admitamos que

, seja verdadeira:

(hipótese da indução)
e provemos que

Temos: (Nessa parte)

Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:

E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:

Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que

seja verdadeiro, e pretendemos provar que também é verdadeiro para

.




Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:

, certo? O autor começou do primeiro membro:

Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:

Que é outra verdade. Agora, com certeza:

Agora, como

é

a

, e este por sua vez é sempre

que

, logo:

Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
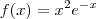 , dizendo quais destes pontos são máximos ou mínimos globais.
, dizendo quais destes pontos são máximos ou mínimos globais.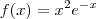
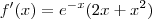
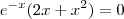
 é sempre positivo, a função só poderá ser zero quando
é sempre positivo, a função só poderá ser zero quando 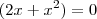 . Portanto as raízes dessa expressão (-2 e 0) serão os pontos críticos.
. Portanto as raízes dessa expressão (-2 e 0) serão os pontos críticos.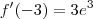 (positivo)
(positivo)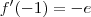 (negativo)
(negativo)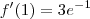 (positivo)
(positivo)


 pela regra
pela regra 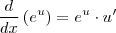 obtemos
obtemos 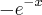 .
.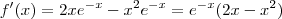
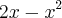 são 0 e 2.
são 0 e 2.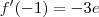 (negativo, portanto decrescente)
(negativo, portanto decrescente)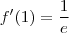 (positivo, portanto crescente)
(positivo, portanto crescente) (negativo, portanto decrescente)
(negativo, portanto decrescente)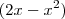 da
da  nem
nem  , que é maior que 2. Portanto, 2 é máximo local.
, que é maior que 2. Portanto, 2 é máximo local.

 .
.

 , seja verdadeira:
, seja verdadeira: (hipótese da indução)
(hipótese da indução)



 seja verdadeiro, e pretendemos provar que também é verdadeiro para
seja verdadeiro, e pretendemos provar que também é verdadeiro para  .
.





 é
é  a
a  , e este por sua vez é sempre
, e este por sua vez é sempre  que
que  , logo:
, logo:
