 por adauto martins » Qua Jul 20, 2016 18:35
por adauto martins » Qua Jul 20, 2016 18:35
mostre que o triangulo de area maxima é isosceles.
soluçao:
dado um triang.qquer,seja x,y,lados e b,base e h altura...
sejam
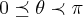
,o angulo q. x faz com b e
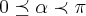
,o angulo q. y faz com a base b...teremos entao,usando a lei dos cossenos q.:
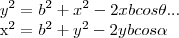
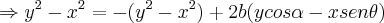
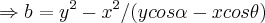
...
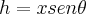
,logo:
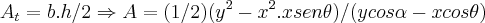
,tomamos entao:
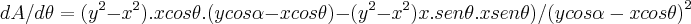
,aqui usei a derivada do quociente...entao para:
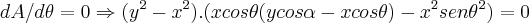
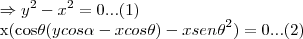
de
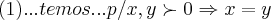
de
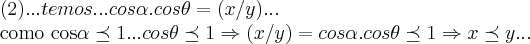
logo por
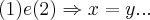
...cqd
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercicio resolvido
por adauto martins » Sex Jul 15, 2016 14:48
- 0 Respostas
- 33701 Exibições
- Última mensagem por adauto martins

Sex Jul 15, 2016 14:48
Teoria dos Números
-
- exercicio resolvido
por adauto martins » Ter Jul 26, 2016 17:43
- 0 Respostas
- 22016 Exibições
- Última mensagem por adauto martins

Ter Jul 26, 2016 17:43
Cálculo: Limites, Derivadas e Integrais
-
- exercicio resolvido
por adauto martins » Sáb Ago 13, 2016 11:28
- 0 Respostas
- 17069 Exibições
- Última mensagem por adauto martins

Sáb Ago 13, 2016 11:28
Teoria dos Números
-
- exercicio resolvido
por adauto martins » Sex Out 18, 2019 14:29
- 2 Respostas
- 22855 Exibições
- Última mensagem por adauto martins

Sex Out 18, 2019 15:42
Trigonometria
-
- exercicio resolvido
por adauto martins » Sáb Out 19, 2019 21:12
- 2 Respostas
- 24348 Exibições
- Última mensagem por adauto martins

Sáb Out 19, 2019 23:51
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
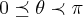 ,o angulo q. x faz com b e
,o angulo q. x faz com b e 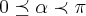 ,o angulo q. y faz com a base b...teremos entao,usando a lei dos cossenos q.:
,o angulo q. y faz com a base b...teremos entao,usando a lei dos cossenos q.: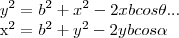
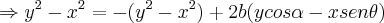
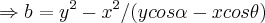 ...
...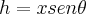 ,logo:
,logo: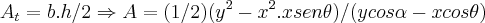 ,tomamos entao:
,tomamos entao: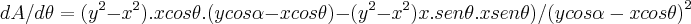 ,aqui usei a derivada do quociente...entao para:
,aqui usei a derivada do quociente...entao para: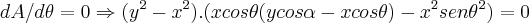
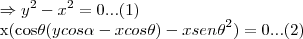
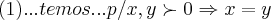
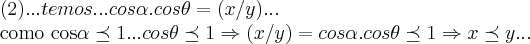
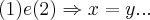 ...cqd
...cqd



 , avisa que eu resolvo.
, avisa que eu resolvo.

