 por klinger1295 » Sex Mai 27, 2016 09:49
por klinger1295 » Sex Mai 27, 2016 09:49
Estou tendo dificuldade para resolver a seguinte questão:
Calcule
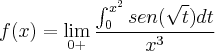
Não sei quais passos devo seguir para resolver este tipo de limite, por isso ainda não cheguei à uma resposta, infelizmente a lista não conta com gabarito também. Agradeço se algum dos senhores puder me ajudar resolvendo esta questão, ou me dando dicas.
-
klinger1295
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mai 27, 2016 09:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Minas
- Andamento: cursando
 por e8group » Seg Jun 06, 2016 21:02
por e8group » Seg Jun 06, 2016 21:02
Este limite apresenta uma indeterminação "0/0" ... Se a regra de L'Hospital for permitida pode derivar o numerador e denominador e verificar se a indeterminação foi eliminada ..Caso persista , continue com o mesmo raciocínio .. Lembre-se que o numerador se exprime como composição de funções deriváveis . Utilize a rega da cadeia + TFC p/ computar a derivada da expressão do numerador ..
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por klinger1295 » Qua Jul 20, 2016 12:50
por klinger1295 » Qua Jul 20, 2016 12:50
e8group escreveu:Este limite apresenta uma indeterminação "0/0" ... Se a regra de L'Hospital for permitida pode derivar o numerador e denominador e verificar se a indeterminação foi eliminada ..Caso persista , continue com o mesmo raciocínio .. Lembre-se que o numerador se exprime como composição de funções deriváveis . Utilize a rega da cadeia + TFC p/ computar a derivada da expressão do numerador ..
Grato, consegui resolver o seguindo estes passos.
-
klinger1295
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Mai 27, 2016 09:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Minas
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo: Limites, Derivadas e Integrais] Cálculo de limites
por jeferson lopes » Ter Mar 26, 2013 08:49
- 2 Respostas
- 5568 Exibições
- Última mensagem por jeferson lopes

Ter Mar 26, 2013 11:52
Cálculo: Limites, Derivadas e Integrais
-
- [limites] exercicio de calculo envolvendo limites
por lucasdemirand » Qua Jul 10, 2013 00:45
- 1 Respostas
- 4812 Exibições
- Última mensagem por e8group

Sáb Jul 20, 2013 13:08
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo 2 - Limites] Existência de Limites
por Piva » Seg Abr 16, 2012 11:29
- 0 Respostas
- 5448 Exibições
- Última mensagem por Piva

Seg Abr 16, 2012 11:29
Cálculo: Limites, Derivadas e Integrais
-
- cálculo de limites
por Hansegon » Seg Ago 25, 2008 11:29
- 2 Respostas
- 59835 Exibições
- Última mensagem por Guill

Dom Abr 08, 2012 16:03
Cálculo: Limites, Derivadas e Integrais
-
- Calculo de limites
por Emanuel_27 » Sáb Nov 01, 2008 01:57
- 3 Respostas
- 7151 Exibições
- Última mensagem por Molina

Qui Abr 09, 2009 22:47
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
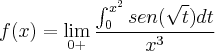



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.