-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478717 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 534888 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 498496 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 714553 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2137097 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por karenfreitas » Qua Mai 04, 2016 14:36
por karenfreitas » Qua Mai 04, 2016 14:36
Calcular o valor de A, onde A =
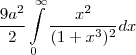
Usar
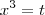
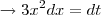
DEsde já agradeço quem puder ajudar a resolver esse problema.
-
karenfreitas
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Mai 04, 2016 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por nakagumahissao » Sex Mai 06, 2016 00:54
por nakagumahissao » Sex Mai 06, 2016 00:54
![A = \frac{9{a}^{2}}{2}\int_{0}^{\infty} \frac{{x}^{2}}{{\left(1+{x}^{3} \right)}^{2}} dx\;\;\;\;\;\;\;[1] A = \frac{9{a}^{2}}{2}\int_{0}^{\infty} \frac{{x}^{2}}{{\left(1+{x}^{3} \right)}^{2}} dx\;\;\;\;\;\;\;[1]](/latexrender/pictures/0d1188185d3c7669e4e5f81f2fef6201.png)
Fazendo-se a substituição:
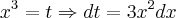
para:

e
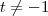
tem-se que:
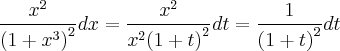
a
integral desta fração seria:
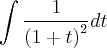
utilizando-se da seguinte substituição
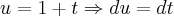
,
poderiamos resolver a
integral acima da seguinte maneira:
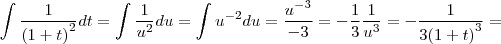
Mas,
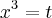
Logo,
![= -\frac{1}{3 {\left(1 + t \right)}^{3}} = -\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}}\;\;\;\;\;\;[2] = -\frac{1}{3 {\left(1 + t \right)}^{3}} = -\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}}\;\;\;\;\;\;[2]](/latexrender/pictures/f3872814f90bb18253c4f3d534a4b133.png)
Finalmente, utilizando-nos dos conhecimentos de
integrais impróprias e usando [2] em 1, teremos:
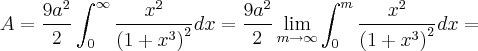
![= \frac{9{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = \frac{9{a}^{2}}{2}\left(-\frac{1}{3} \right) \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = = \frac{9{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = \frac{9{a}^{2}}{2}\left(-\frac{1}{3} \right) \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] =](/latexrender/pictures/8c34ed89eae65f025bdfb7e00086b594.png)
![= -\frac{3{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = -\frac{3{a}^{2}}{2}\left(-0 + 1 \right) = -\frac{3{a}^{2}}{2} = -\frac{3{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = -\frac{3{a}^{2}}{2}\left(-0 + 1 \right) = -\frac{3{a}^{2}}{2}](/latexrender/pictures/d86c57d5afb1790a8408b296a56e5e4f.png)
Que é o resultado procurado, portanto:
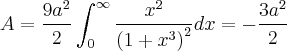
Espero não ter errado nos cáculos, mas a idéia básica é essa.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo] Calculando uma integral imprópria com uma condição
por karenfreitas » Sex Mai 06, 2016 15:10
- 0 Respostas
- 1835 Exibições
- Última mensagem por karenfreitas

Sex Mai 06, 2016 15:10
Cálculo: Limites, Derivadas e Integrais
-
- Calcular o seguinte limite
por RodrigoMan » Qua Jun 06, 2012 14:30
- 2 Respostas
- 2087 Exibições
- Última mensagem por RodrigoMan

Qua Jun 06, 2012 16:44
Cálculo: Limites, Derivadas e Integrais
-
- Como calcular porcentagem do seguinte valor:?
por icaro » Ter Jan 23, 2018 12:23
- 1 Respostas
- 7326 Exibições
- Última mensagem por DanielFerreira

Qui Jan 25, 2018 11:31
Aritmética
-
- Gostaria de saber como calcular o seguinte limite
por felipe_08 » Qui Abr 23, 2015 17:36
- 2 Respostas
- 2234 Exibições
- Última mensagem por felipe_08

Qui Abr 23, 2015 22:51
Cálculo: Limites, Derivadas e Integrais
-
- Integral Imprópria
por CrazzyVi » Seg Set 27, 2010 17:13
- 5 Respostas
- 6315 Exibições
- Última mensagem por menino de ouro

Qui Jan 24, 2013 13:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 58 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
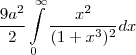
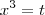
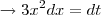

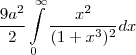
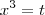
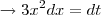

![A = \frac{9{a}^{2}}{2}\int_{0}^{\infty} \frac{{x}^{2}}{{\left(1+{x}^{3} \right)}^{2}} dx\;\;\;\;\;\;\;[1] A = \frac{9{a}^{2}}{2}\int_{0}^{\infty} \frac{{x}^{2}}{{\left(1+{x}^{3} \right)}^{2}} dx\;\;\;\;\;\;\;[1]](/latexrender/pictures/0d1188185d3c7669e4e5f81f2fef6201.png)
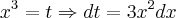

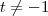
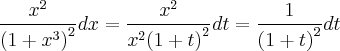
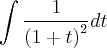
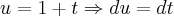 ,
,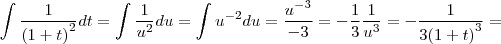
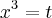
![= -\frac{1}{3 {\left(1 + t \right)}^{3}} = -\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}}\;\;\;\;\;\;[2] = -\frac{1}{3 {\left(1 + t \right)}^{3}} = -\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}}\;\;\;\;\;\;[2]](/latexrender/pictures/f3872814f90bb18253c4f3d534a4b133.png)
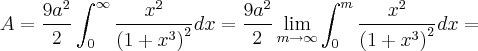
![= \frac{9{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = \frac{9{a}^{2}}{2}\left(-\frac{1}{3} \right) \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = = \frac{9{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = \frac{9{a}^{2}}{2}\left(-\frac{1}{3} \right) \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] =](/latexrender/pictures/8c34ed89eae65f025bdfb7e00086b594.png)
![= -\frac{3{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = -\frac{3{a}^{2}}{2}\left(-0 + 1 \right) = -\frac{3{a}^{2}}{2} = -\frac{3{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = -\frac{3{a}^{2}}{2}\left(-0 + 1 \right) = -\frac{3{a}^{2}}{2}](/latexrender/pictures/d86c57d5afb1790a8408b296a56e5e4f.png)
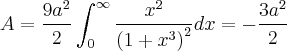

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.