 por Eletrica07 » Ter Mar 29, 2016 15:48
por Eletrica07 » Ter Mar 29, 2016 15:48
Boa tarde pessoal, estou com dúvida para calcular o laplaciano desta expressão:

A dúvida acontece quando vou derivar a primeira vez em relação ao x segundo uma tabela que tenho aqui dada pelo professor deve-se usar a seguinte regra :
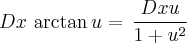
, então eu uso esta regra e chego no seguinte:
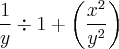
, mas quando faço essa derivação no symbolab ou vejo a resolução na internet o resultado da o seguinte:
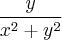
. Alguém por favor poderia me dar uma explicação mais detalhada?
-
Eletrica07
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mar 29, 2016 14:06
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por adauto martins » Qua Mar 30, 2016 13:31
por adauto martins » Qua Mar 30, 2016 13:31
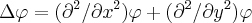
...
1)em relaçao a x,
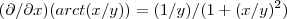
...
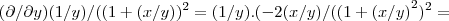
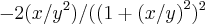
2)em relaçao a y,
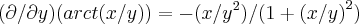
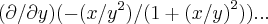
haja calculo,termine ai...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema do Laplaciano?
por Jhenrique » Qui Fev 13, 2014 10:28
- 0 Respostas
- 745 Exibições
- Última mensagem por Jhenrique

Qui Fev 13, 2014 10:28
Geometria Analítica
-
- Matriz hessiana e Laplaciano de gauss
por irado » Qui Out 07, 2010 22:38
- 0 Respostas
- 1857 Exibições
- Última mensagem por irado

Qui Out 07, 2010 22:38
Cálculo: Limites, Derivadas e Integrais
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4592 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- DADA A FUNÇÃO
por SILMARAKNETSCH » Sex Nov 09, 2012 15:29
- 5 Respostas
- 2846 Exibições
- Última mensagem por SILMARAKNETSCH

Sex Nov 09, 2012 16:50
Funções
-
- [Função] Dada a função, determine as constantes
por Raphael Leal » Qua Abr 02, 2014 16:42
- 1 Respostas
- 2361 Exibições
- Última mensagem por rodrigorc

Qua Abr 02, 2014 18:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

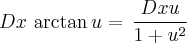 , então eu uso esta regra e chego no seguinte:
, então eu uso esta regra e chego no seguinte: 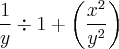 , mas quando faço essa derivação no symbolab ou vejo a resolução na internet o resultado da o seguinte:
, mas quando faço essa derivação no symbolab ou vejo a resolução na internet o resultado da o seguinte: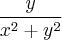 . Alguém por favor poderia me dar uma explicação mais detalhada?
. Alguém por favor poderia me dar uma explicação mais detalhada?

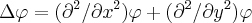 ...
...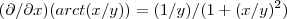 ...
...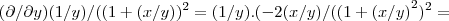
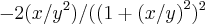
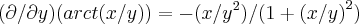
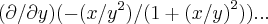 haja calculo,termine ai...
haja calculo,termine ai...

 .
.



