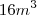. Encontre as dimensões que produzem a caixa de menor menor custo, se o material utilizado nas laterais custa metade do utilizado no fundo e na tampa. Dúvida:
O enunciado desse problema está correcto ? É possível, tal como está, chegar a qualquer resolução ?
Se sim, como ?
É que acho o enunciado confuso.
O que se pretende saber?
Apenas as dimensões e uma caixa rectangular de volume igual a
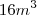que possa ser construída com o menor material possível ?Parece-me que não, porque o enunciado pede para encontrar as dimensões que produzem a caixa de menor custo se o material utilizado nas laterais custa metade do utilizado no fundo e na tampa.
Assim sendo, não deveriam ser dados pelo menos um dos preços dos materiais ? Da lateral ou do fundo/tampa ?
Abaixo seguem três links de vidios sobre questões idênticas, que talvez possam ajudar a esclarecer a minha dúvida.
https://www.youtube.com/watch?v=oCR4vvtjGMw
(Neste caso é uma caixa, só que reforçada em 4 camadas no fundo, 1 na tampa, e 2 dos lados. Como ficaria a resolução se todos os lados fossem simples ?)
https://www.youtube.com/watch?v=32a1Kg0SicU
(Neste caso é um cilindro com materiais com preços diferentes para a lateral e (base + tampa). No caso de serem dados preços no enunciado que postei,tal como os que são dados neste vídeo, como ficaria a resolução em relação à caixa ?)
https://www.youtube.com/watch?v=Gp2OQaVOTNY
( Ver Exemplo 3 aos 32:36 m. Este problema é por meio de derivada, mas a a caixa tem base quadrada ou seja: x = y)
Ou seja:
Eu desejava que alguém me indicasse o método ou equação mais adequada para as duas situações.
Para encontrar as dimensões, e só as dimensões, da caixa, sem preços incorporados na equação.
Ou, se houver um modo de equacionar o problema onde se possa incorporar os preços logo na resolução, tal como no caso do vídeo do cilindro, com os preços já incorporados.
Ou talvez não seja necessária esta última versão, visto que, ao se obter as dimensões da caixa, acham-se a área dos lados, somam-se dois a dois e multiplicam-se pelo respectivos preços; ou sua metade, ou seu o dobro, consoante o preço que for dado, ou o das laterais ou o da tampa/fundo, somam-se e obtém-se o custo. Isto evidentemente, supondo que eram dados preços no enunciado.
Grato pela atenção
Armando
por 
