-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 481153 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 543710 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 507490 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 738561 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2186958 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por kjelin » Ter Fev 02, 2016 01:39
por kjelin » Ter Fev 02, 2016 01:39
Sabe-se que f??(x) = xlnx e que f?(1) = f(1) = 0. Calcule f(x).
-
kjelin
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Fev 02, 2016 01:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharelado em química
- Andamento: cursando
 por DanielFerreira » Seg Fev 08, 2016 16:47
por DanielFerreira » Seg Fev 08, 2016 16:47
Olá
Kjelin, seja bem-vindo!
De acordo com o enunciado,
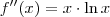
; se integrarmos cada lado da igualdade ficamos com
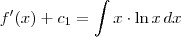
.
Encontramos a função derivada primeira resolvendo a
integral 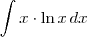
por partes.
Considerando

e
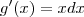
temos que:
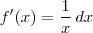
e
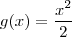
.
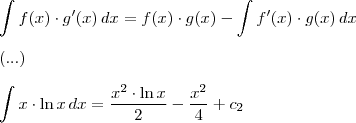
Por conseguinte,
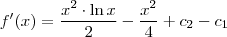
.
Da condição
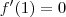
, tiramos que
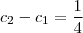
. Então, temos que:
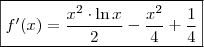
.
A fim de encontrar a função

, aplicamos raciocínio análogo ao anterior; ou seja, integramos cada lado da igualdade...
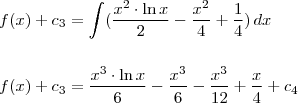
Obs1.: o primeiro termo do integrando acima foi obtido aplicando uma nova integração por partes;
Obs2.: de
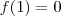
, tiramos que
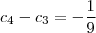
.
Por fim, concluímos que
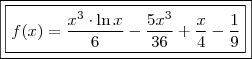
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- P.G., calcule Sn=9+99+999... +10n-1
por georgefdfdl » Qui Nov 10, 2011 23:49
- 1 Respostas
- 1369 Exibições
- Última mensagem por LuizAquino

Sex Nov 11, 2011 17:41
Progressões
-
- calcule y
por Guilhermme » Sáb Mar 31, 2012 17:06
- 4 Respostas
- 3583 Exibições
- Última mensagem por Nico Romani

Qui Mar 31, 2016 17:01
Geometria Analítica
-
- Calcule a e b
por andersontricordiano » Dom Mar 02, 2014 12:01
- 3 Respostas
- 4196 Exibições
- Última mensagem por nat-larissa

Seg Mar 03, 2014 20:12
Sistemas de Equações
-
- Calcule
por andersontricordiano » Ter Mar 18, 2014 00:34
- 1 Respostas
- 1707 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 06, 2016 11:38
Aritmética
-
- Calcule o 1º termo
 por Cleyson007 » Dom Dez 27, 2009 13:47
por Cleyson007 » Dom Dez 27, 2009 13:47
- 1 Respostas
- 1829 Exibições
- Última mensagem por Lucio Carvalho

Seg Dez 28, 2009 09:46
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



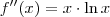 ; se integrarmos cada lado da igualdade ficamos com
; se integrarmos cada lado da igualdade ficamos com 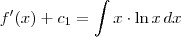 .
.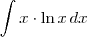 por partes.
por partes. e
e 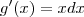 temos que:
temos que: 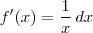 e
e 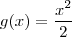 .
.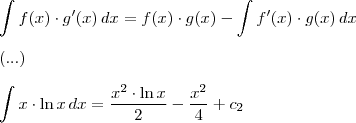
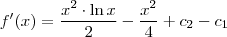 .
. 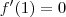 , tiramos que
, tiramos que 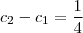 . Então, temos que:
. Então, temos que: 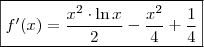 .
. , aplicamos raciocínio análogo ao anterior; ou seja, integramos cada lado da igualdade...
, aplicamos raciocínio análogo ao anterior; ou seja, integramos cada lado da igualdade...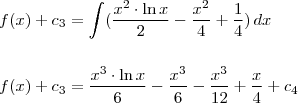
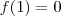 , tiramos que
, tiramos que 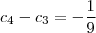 .
.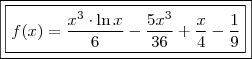

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.