A questão pede para dar exemplos de limites que existem e limites que não existem nas seguintes indeterminações:
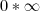
- Eu usei os seguintes limites, quero conferir se está certo:
limites
Existe:
Está dando erro... Então vou colocar sem a tag tex, ele não está conseguindo fazer a fração de 2x/x
lim_{x\to\infty } \frac{2x}{x} = 0
Não existe:
lim_{x\to\infty }\frac{\sqrt{x}}{x}
limites
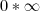
Existe:
lim_{x\to\0 }\frac{1}{x} * x = 1
Não existe:
lim_{x\to\0 }\frac{\sqrt{x}}{x^2} * x
limites
lim_{x\to\ {h} }\frac{\sqrt[2]{9 + h} - 3}{{h}}
lim_{x\to\ 0 }\frac{x^2 * {\sqrt{x}} }{x}
limites
- lim_{x\to\ \infty }\sqrt{x + 5} - \sqrt{x}
lim_{x\to\ \infty }x - \sqrt{x}
Novamente peço desculpas por não usar as tags, mas está dando erro para quase tudo que tento inserir (e funciona em outro editor)
.
