Mostre que a equação tem exatamente uma raiz real
a- 2x+ cosx=0 b-x³ +e^x=0
Nota- nao sei nem como inicia



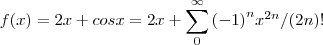 ,aqui vamos tomar a menor potencia menor ou igual a potencia do polinomio em questao,no caso x...logo...
,aqui vamos tomar a menor potencia menor ou igual a potencia do polinomio em questao,no caso x...logo...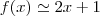 ,pois
,pois 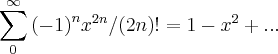 ...utilizando a regra de descartes p/raizes teremos...
...utilizando a regra de descartes p/raizes teremos...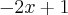 ,uma mudança p/x negativo...logo existe uma unica raiz real,e negativa p/f(x)...
,uma mudança p/x negativo...logo existe uma unica raiz real,e negativa p/f(x)...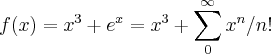 ...vamos tomar entao:
...vamos tomar entao: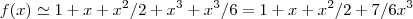 ...usando a regra de descartes,nao ha troca de sinais dos coeficientes de f(x) p/x positivo...p/x negativo,existem duas trocas de sinais....como f(x) é um polinomio de grau igual a tres deveriamos ter tres raizes(reais ou complexas),o q. nos leva a deduzir q. existe uma raioz real negativa e duas raizes complexas(conjugadas)...
...usando a regra de descartes,nao ha troca de sinais dos coeficientes de f(x) p/x positivo...p/x negativo,existem duas trocas de sinais....como f(x) é um polinomio de grau igual a tres deveriamos ter tres raizes(reais ou complexas),o q. nos leva a deduzir q. existe uma raioz real negativa e duas raizes complexas(conjugadas)...
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

