-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478851 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 536144 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 499795 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 718210 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2143507 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Mendes » Dom Ago 23, 2015 15:10
por Mendes » Dom Ago 23, 2015 15:10
Enunciado:
Um engenheiro resolveu construir uma escada na sua casa que possuia dois andares, mas teve dúvida na construção do corrimão porque as duas escadas formavam dois arcos. Sabendo que o corrimão começa com a escada e que de uma escada para outra o arco faz um giro. Determine a função, os pontos de início e fim de cada arco para cada andar, sabendo que a altura não pode ultrapassar 1m e que esses dois arcos formam uma parábola semicúbica e que o comprimento não pode ultrapassar 5 unidades de comprimento.
Eu sei que terei que somar a
integral das duas funções, e também sei que as
integrais vão de 0 a 1 e de 1 a 2 respectivamente, para respeitar a altura de 1m.
Pela definição de parábola semicúbica temos que
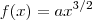
Fonte:
https://pt.wikipedia.org/wiki/Par%C3%A1 ... %C3%BAbicaSegue em anexo um esboço do que eu consegui deduzir num gráfico. Não sei se está certo, mas foi o que eu tentei.
Dúvida: Eu queria saber como deduzir as funções solicitadas? Não sei por onde começar

- Anexos
-
![questao[1].jpg (815.12 KiB) Exibido 1288 vezes questao[1].jpg](./download/file.php?id=2325&t=1&sid=28a813e1fa802dd37129cc9c65462143)
- Esboço de gráfico
-
Mendes
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Ago 23, 2015 11:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Exatas/Sistemas de Informação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- comprimento do arco
por liviabgomes » Seg Mai 30, 2011 16:11
- 10 Respostas
- 5363 Exibições
- Última mensagem por liviabgomes

Qua Jun 01, 2011 15:03
Cálculo: Limites, Derivadas e Integrais
-
- comprimento de arco
por manuoliveira » Ter Out 23, 2012 19:43
- 0 Respostas
- 1047 Exibições
- Última mensagem por manuoliveira

Ter Out 23, 2012 19:43
Cálculo: Limites, Derivadas e Integrais
-
- comprimento do arco
por VenomForm » Seg Mai 20, 2013 13:29
- 0 Respostas
- 1028 Exibições
- Última mensagem por VenomForm

Seg Mai 20, 2013 13:29
Cálculo: Limites, Derivadas e Integrais
-
- Calculo do comprimento do arco.
por brunojorge29 » Seg Abr 23, 2012 11:21
- 3 Respostas
- 2366 Exibições
- Última mensagem por Russman

Seg Abr 23, 2012 22:32
Cálculo: Limites, Derivadas e Integrais
-
- Comprimento do arco!! Urgente!!
por manuoliveira » Ter Out 23, 2012 20:34
- 4 Respostas
- 2786 Exibições
- Última mensagem por manuoliveira

Ter Out 23, 2012 21:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 134 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.