 por gdarius » Ter Mar 16, 2010 15:57
por gdarius » Ter Mar 16, 2010 15:57
-
gdarius
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Ago 15, 2009 23:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
 por Elcioschin » Ter Mar 16, 2010 23:26
por Elcioschin » Ter Mar 16, 2010 23:26
Por acaso a solução é: -(1/2)*ln[(x - 2 + V3)/(x - 2 - V3)] ?
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por gdarius » Qua Mar 17, 2010 18:54
por gdarius » Qua Mar 17, 2010 18:54
A solução é esta, mas o meu problema é qto ao desenvolvimento de onde eu enviei até a resposta.
-
gdarius
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Ago 15, 2009 23:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
 por gdarius » Qua Mar 17, 2010 19:00
por gdarius » Qua Mar 17, 2010 19:00
Elcioschin escreveu:Por acaso a solução é: -(1/2)*ln[(x - 2 + V3)/(x - 2 - V3)] ?
Elcioschin, tô com problema no latex, baixei e instalaei de acordo com as instruções, só que, qdo executo qq arquivo recebo a mensagem de erro(demo - 2 erro(s), 0 aviso(s), 0 overfull box(es), 0 underfull box(es)).
Se vc puder me ajudar fico grato.
-
gdarius
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sáb Ago 15, 2009 23:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: cursando
 por Elcioschin » Qua Mar 17, 2010 21:16
por Elcioschin » Qua Mar 17, 2010 21:16
gdarius
Infelizmente não sei usar o LaTeX, portanto não tenho como ajudá-lo
Continunado de onde vc parou:
Int 3/[(x - 2)² - 3] dx ----> Fazendo u = x - 2 ----> du = dx ----> fazendo 3 = (V3)² = V3*V3
Int V3*V3/[u² - (V3)²] du ----> Colocando V3 para fora do sinal de integral:
V3*Int V3/[u² - (V3)²] du
Procure em qualquer livro de cálculo: Int a/[u² - a²] du = (- 1/2a) ln[(u + a)/(u - a)]
Aplique no seu problema e chegará na minha solução
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por DanielFerreira » Sáb Mar 31, 2012 19:32
por DanielFerreira » Sáb Mar 31, 2012 19:32
Elcioschin escreveu:gdarius
Infelizmente não sei usar o LaTeX, portanto não tenho como ajudá-lo
Continunado de onde vc parou:

----> Fazendo u = x - 2 ----> du = dx ----> fazendo 3 =
![(\sqrt[]{3})^2 (\sqrt[]{3})^2](/latexrender/pictures/2e5bbf992f084f4a89fcdc9c145cd3d2.png)
=
![\sqrt[]{3} . \sqrt[]{3} \sqrt[]{3} . \sqrt[]{3}](/latexrender/pictures/f0995320f69022e22726fa7b203caad8.png)
![\int_{}^{}\frac{\sqrt[]{3}.\sqrt[]{3}}{u^2 - (\sqrt[]{3})^2} \int_{}^{}\frac{\sqrt[]{3}.\sqrt[]{3}}{u^2 - (\sqrt[]{3})^2}](/latexrender/pictures/5a4f409520dab186a398cb3bb7aeed55.png)
du ----> Colocando
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png)
para fora do sinal de integral:
![\sqrt[]{3}\int_{}^{}\frac{\sqrt[]{3}}{u^2 - (\sqrt[]{3})^2} \sqrt[]{3}\int_{}^{}\frac{\sqrt[]{3}}{u^2 - (\sqrt[]{3})^2}](/latexrender/pictures/16c88e372e512f1d2686195f881f68a9.png)
du
Procure em qualquer livro de cálculo:
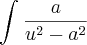
du =
![- \frac{1}{2a} . ln\left[\frac{u + a}{u - a} \right] - \frac{1}{2a} . ln\left[\frac{u + a}{u - a} \right]](/latexrender/pictures/a38024fa88924f8b7d9c6289be0c09dc.png)
Aplique no seu problema e chegará na minha solução
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral indefinida
 por CrazzyVi » Ter Ago 17, 2010 21:41
por CrazzyVi » Ter Ago 17, 2010 21:41
- 1 Respostas
- 2714 Exibições
- Última mensagem por Lucio Carvalho

Qua Ago 18, 2010 08:27
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida
por felipealves » Ter Jun 21, 2011 11:48
- 3 Respostas
- 3992 Exibições
- Última mensagem por felipealves

Ter Jun 21, 2011 20:59
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] indefinida
por Aliocha Karamazov » Qui Mar 01, 2012 20:30
- 7 Respostas
- 5057 Exibições
- Última mensagem por Aliocha Karamazov

Sáb Mar 03, 2012 21:59
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida - 2
por DanielFerreira » Sáb Mar 31, 2012 18:31
- 1 Respostas
- 2072 Exibições
- Última mensagem por LuizAquino

Sáb Mar 31, 2012 18:53
Cálculo: Limites, Derivadas e Integrais
-
- Integral indefinida - 3
por DanielFerreira » Sáb Mar 31, 2012 18:41
- 2 Respostas
- 2097 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 19:20
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![[tex]\int_{} \frac{3}{{x}^{2}-4x+1}dx [tex]\int_{} \frac{3}{{x}^{2}-4x+1}dx](/latexrender/pictures/d3ce5d1daee014fe6f256ff294cc8c56.png)
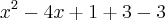
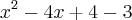
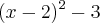
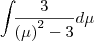

![[tex]\int_{} \frac{3}{{x}^{2}-4x+1}dx [tex]\int_{} \frac{3}{{x}^{2}-4x+1}dx](/latexrender/pictures/d3ce5d1daee014fe6f256ff294cc8c56.png)
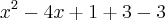
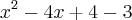
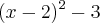
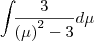





----> Fazendo u = x - 2 ----> du = dx ----> fazendo 3 =
=
du ----> Colocando
para fora do sinal de integral:
du
du =
![- \frac{1}{2a} . ln\left[\frac{u + a}{u - a} \right] - \frac{1}{2a} . ln\left[\frac{u + a}{u - a} \right]](/latexrender/pictures/a38024fa88924f8b7d9c6289be0c09dc.png)



 , avisa que eu resolvo.
, avisa que eu resolvo.

