Bom dia!
Gostaria de pedir a ajuda de alguém para resolver essa questão.
Antes de mais nada, gostaria de dizer que se trata de provar o limite por épsilon e delta.
Estou tendo uma dificuldade enorme, pois envolve restrição de intervalo e eu ainda não consegui compreender essa parte do assunto.
Aqui vai: limite de 9/x+1 quando x tende a 2=3
Comecei assim: Queremos provar que para todo £>0, existe um s>0 tal que 0<x-2<s, então 9/x+1 -3< £.
|(9/x+1) -3| < £ ==> |9-3x-3/x+1| < £ ==>|-3x + 6/x+1| < £ ==> |-3(x-2)/x+1| < £
Como na desigualdade há (x+1) do qual nada se conhece, necessita-se restringir s de modo que encontremos um desigualdade envolvendo-o.
Tomei s < ou = 1 e fiz: -s< x-2 < s ===> -s+2 < x < s+2 ===> 1< x < 3
logo 2< x+1 < 4
Agora, se 0< x-2 < s e x+1<4 , então:
|-3(x-2)/x+1| < 4s ===> |-3| |x-2/x+1| <4s
Nessa parte foi que eu travei. Não sei se em alguma parte eu errei.
Por favor, me ajudem.
Caso possam explicar um pouco sobre como proceder no caso de se fazer necessário restringir, eu iria agradecer muito.


 por um numero positivo , por conseguinte majoraremos
por um numero positivo , por conseguinte majoraremos 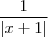 .
. 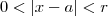 então
então 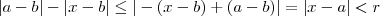 donde tem-se
donde tem-se 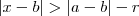 , substituindo a e b pelos valores em interesse , vamos obter
, substituindo a e b pelos valores em interesse , vamos obter 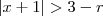 . Veja que sempre que tomarmos 0<r <3 , vamos ter a minoração desejada , destes r> 0 , satisfazendo a propriedade , restringiremos tal arbitrariedade , escolhendo-se um particular(aqui é o nosso
. Veja que sempre que tomarmos 0<r <3 , vamos ter a minoração desejada , destes r> 0 , satisfazendo a propriedade , restringiremos tal arbitrariedade , escolhendo-se um particular(aqui é o nosso 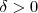 ) para cada
) para cada 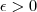 dado, de modo que
dado, de modo que 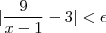 sempre que
sempre que 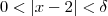 .
. 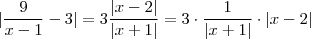 . Assim, se
. Assim, se 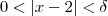 , vamos ter
, vamos ter 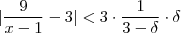 . Gostaríamos que delta fosse tal que
. Gostaríamos que delta fosse tal que 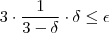 , e sendo temos ,
, e sendo temos , 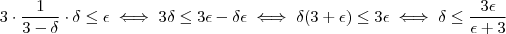 .
.

 .
.



