estou com uma dúvida ao resolver a seguinte integral:
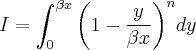
onde
 e x são constantes.
e x são constantes.Bem, se n for um número RACIONAL diferente de -1, pode-se fazer da seguinte maneira:
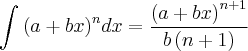
e assim, teria como resultado daquela integral o seguinte:
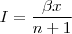
Porém, n tem o valor de:
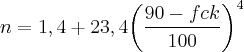
onde fck varia de 50 a 90, podendo assumir valor IRRACIONAL. Por exemplo, quando fck é igual a 60, n é igual a 1,58954.
Enfim, minha dúvida é se eu posso integrar como fiz acima ou se tenho de usar exponencial (
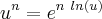 ), séries infinitas ou outro artifício por conta de n ser IRRACIONAL. E, como deveria resolver esta integral?
), séries infinitas ou outro artifício por conta de n ser IRRACIONAL. E, como deveria resolver esta integral?Desde já agradeço!!!



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.