 por neoreload » Dom Nov 09, 2014 00:36
por neoreload » Dom Nov 09, 2014 00:36
Pessoal preciso de ajuda nessa questão:
Calcular integral usando método da substituição:
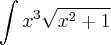
Utilizando a substituição simples pelo U, nada de tg ainda ^^.
Eu tentei fazer varias vezes, mas nunca consigo sair do começo quando eu tento substituir e chego eim:
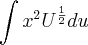
. Agradeço muito quem puder deixar o passo a passo o mais detalhado possível. pq como eu disse, me perdi todo mesmo :(
-
neoreload
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Sáb Ago 09, 2014 16:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Dom Nov 09, 2014 02:02
por e8group » Dom Nov 09, 2014 02:02
Basta fazer u =x^2 + 1 ; Daí a última integral q escrevesse fica
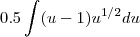
, pls corrija ...boa sorte !
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por neoreload » Dom Nov 09, 2014 03:16
por neoreload » Dom Nov 09, 2014 03:16
santhiago escreveu:Basta fazer u =x^2 + 1 ; Daí a última integral q escrevesse fica
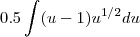
, pls corrija ...boa sorte !
mas pra onde foi o x³? e como vc colocou u-1?
-
neoreload
- Usuário Dedicado

-
- Mensagens: 27
- Registrado em: Sáb Ago 09, 2014 16:15
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Dom Nov 09, 2014 12:57
por e8group » Dom Nov 09, 2014 12:57
Como

então
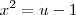
. Observe também que

ou seja
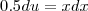
. Deste modo ,

-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] usando método da substituição
por neoreload » Sex Nov 14, 2014 02:43
- 0 Respostas
- 1560 Exibições
- Última mensagem por neoreload

Sex Nov 14, 2014 02:43
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Método da Substituição
por raimundoocjr » Sáb Jul 27, 2013 13:04
- 2 Respostas
- 2013 Exibições
- Última mensagem por raimundoocjr

Sáb Jul 27, 2013 18:02
Cálculo: Limites, Derivadas e Integrais
-
- [Integral Indefinida] Método por Substituição
por Matheus Lacombe O » Sáb Mar 02, 2013 23:54
- 3 Respostas
- 3011 Exibições
- Última mensagem por e8group

Dom Mar 03, 2013 18:15
Cálculo: Limites, Derivadas e Integrais
-
- Integração Usando Substituição t = tan Teta/2
por cferreira264 » Dom Jul 02, 2017 19:27
- 0 Respostas
- 1412 Exibições
- Última mensagem por cferreira264

Dom Jul 02, 2017 19:27
Cálculo: Limites, Derivadas e Integrais
-
- [Usando tecnicas de integrais por substituiçao simples]
por menino de ouro » Qua Out 24, 2012 23:10
- 1 Respostas
- 1683 Exibições
- Última mensagem por MarceloFantini

Qui Out 25, 2012 01:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
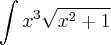
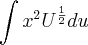 . Agradeço muito quem puder deixar o passo a passo o mais detalhado possível. pq como eu disse, me perdi todo mesmo :(
. Agradeço muito quem puder deixar o passo a passo o mais detalhado possível. pq como eu disse, me perdi todo mesmo :(

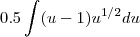 , pls corrija ...boa sorte !
, pls corrija ...boa sorte !
 então
então 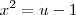 . Observe também que
. Observe também que  ou seja
ou seja 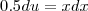 . Deste modo ,
. Deste modo , 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.