Estou com uma dúvida quanto a derivação da equação que representa o Volume na questão seguinte, e se possível postarem um gabarito para eu corrigir com a minha, ficaria grato.
Drenagem de um reservatório hemisférico. Água escoa a uma taxa de 6m^3/min de um reservatório hemisférico com raio de 13m, mostrado aqui em perfil. Responda as questões a seguir, sendo o volume da água em um recipiente hemisférico de raio r dado por (não vou usar o Latex por falta de treino e tempo no momento !) V=(pi/3).y².(3R-y), quando a água tiver y metros de profundidade.
pois bem, a letra é pede a taxa de variação quando a profundidade for 8 metros, e pare isso fui derivar a fórmula de Volume, mas não consegui (acho que não!) e por isso peço a ajuda de vocês, obrigado !
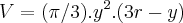...dV/dt=
...
...
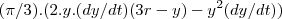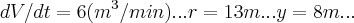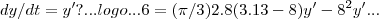...termine o CALCULO!,ou seja faça as contas...
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)