 por b11adriano » Sáb Out 04, 2014 14:56
por b11adriano » Sáb Out 04, 2014 14:56
Nao estou conseguindo a resolução de problema:
Uma placa circular plana tem o formato da região x^2 + y^2 ?1. A placa, incluindo a
fronteira na qual x^2 + y^2 =1 é aquecida, de forma que a temperatura no ponto (x,y)
é dada pela equação T(x, y)= x^2 + 2y^2 ? x . Encontre as temperaturas nos pontos
mais quentes e mais frios da placa?
-
b11adriano
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Out 04, 2014 14:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: egenharia de produçao
- Andamento: cursando
 por adauto martins » Seg Out 06, 2014 12:40
por adauto martins » Seg Out 06, 2014 12:40
de forma sucinta,teremos:
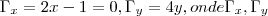
sao as derivadas parciais em relaçao a x,y
resolvendo temos:(1/2,0)um ponto de max. ou min...
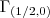
=-1/2...
(1/2,0)e ponto min.,pois
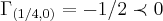
e
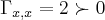
,onde
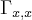
e a derivada segunda no ponto (1/2,0)...vamos procurar a direçao do gradiente,onde a funçao procura seu max...entao:
tomemos H=(cosa,sena) tal q.
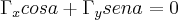

tga=-
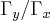

a=arctg(-(4y/(2x-1)),agora sao alguns calculos,observando a

(
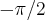
,
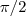
)e
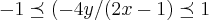
,faz-se os calculos achando a e subst. na expressao do gradiente,tem-se o ponto de max. e o valor da temp. max...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Marcos Ueder » Qui Set 17, 2015 18:09
por Marcos Ueder » Qui Set 17, 2015 18:09
Poderia me ajudar com essa questão...eu não conseguir entender como vcs encontraram a direção do gradiente. Obrigado
-
Marcos Ueder
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Set 17, 2015 17:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia eletrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ponto Máximo e Mínimo de uma função.
por lucasowner » Qui Ago 13, 2015 03:05
- 1 Respostas
- 2010 Exibições
- Última mensagem por nakagumahissao

Qui Ago 13, 2015 15:29
Cálculo: Limites, Derivadas e Integrais
-
- [Ponto máximo de uma função]- Pressão sanguínea.
por alicemneves » Seg Mai 28, 2012 00:20
- 7 Respostas
- 5371 Exibições
- Última mensagem por Russman

Qui Mai 31, 2012 22:58
Cálculo: Limites, Derivadas e Integrais
-
- [Dúvida] Integral e ponto máximo de uma função
por ruisu » Seg Mar 04, 2013 15:19
- 1 Respostas
- 1577 Exibições
- Última mensagem por young_jedi

Seg Mar 04, 2013 23:14
Cálculo: Limites, Derivadas e Integrais
-
- [Máximo e Mínimos]
por dehcalegari » Qui Jun 20, 2013 18:58
- 2 Respostas
- 8768 Exibições
- Última mensagem por dehcalegari

Qui Jun 20, 2013 22:47
Cálculo: Limites, Derivadas e Integrais
-
- maximo e minimos relativo
por matematica_mat » Sáb Out 29, 2011 13:05
- 0 Respostas
- 1739 Exibições
- Última mensagem por matematica_mat

Sáb Out 29, 2011 13:05
Cálculo Numérico e Aplicações
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


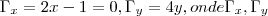 sao as derivadas parciais em relaçao a x,y
sao as derivadas parciais em relaçao a x,y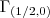 =-1/2...
=-1/2...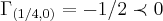 e
e 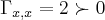 ,onde
,onde 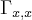 e a derivada segunda no ponto (1/2,0)...vamos procurar a direçao do gradiente,onde a funçao procura seu max...entao:
e a derivada segunda no ponto (1/2,0)...vamos procurar a direçao do gradiente,onde a funçao procura seu max...entao: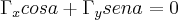

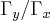
 (
(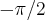 ,
,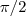 )e
)e 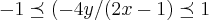 ,faz-se os calculos achando a e subst. na expressao do gradiente,tem-se o ponto de max. e o valor da temp. max...
,faz-se os calculos achando a e subst. na expressao do gradiente,tem-se o ponto de max. e o valor da temp. max...