-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478226 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 532379 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495886 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 707298 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2124367 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Pessoa Estranha » Qui Set 25, 2014 13:03
por Pessoa Estranha » Qui Set 25, 2014 13:03
Olá!
Preciso de ajuda para resolver o seguinte exercício:
"Obter a equação da reta tangente à curva
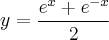
em

".
Minha resolução:
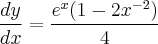
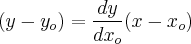
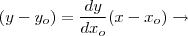
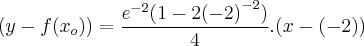
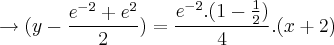
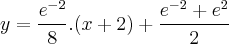
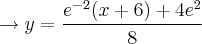
Resposta do Livro:
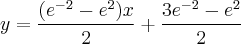
Tentei fazer algumas manipulações algébricas para tentar chegar numa equivalência das expressões, mas não deu certo.
Por favor, podem me ajudar?
Muito Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por DanielFerreira » Qui Set 25, 2014 21:57
por DanielFerreira » Qui Set 25, 2014 21:57
Derivemos,
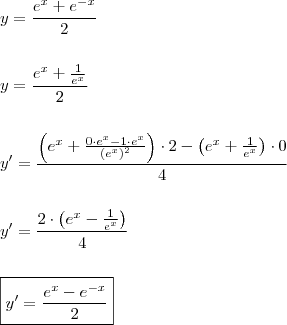
Sabemos que a equação da reta tangente... no ponto

é dada por

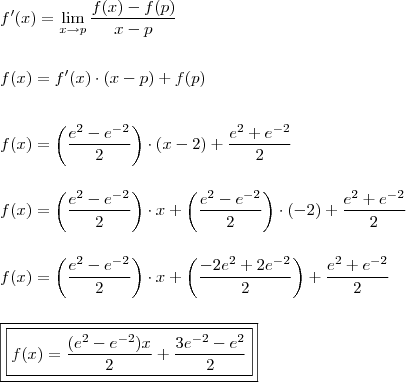
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1728
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Engº Pedreira - Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Pessoa Estranha » Sex Set 26, 2014 10:47
por Pessoa Estranha » Sex Set 26, 2014 10:47
Olá! Muito Obrigada! Errei em alguma coisa na hora de derivar. Vou ver direitinho agora. Muito obrigada mesmo!

-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- cálculo diferencial e integral
por Neperiano » Qua Out 08, 2008 22:20
- 4 Respostas
- 6549 Exibições
- Última mensagem por admin

Ter Out 14, 2008 16:41
Cálculo: Limites, Derivadas e Integrais
-
- calculo integral e diferencial
 por edilainemorais » Qui Fev 20, 2014 18:15
por edilainemorais » Qui Fev 20, 2014 18:15
- 0 Respostas
- 1574 Exibições
- Última mensagem por edilainemorais

Qui Fev 20, 2014 18:15
Cálculo: Limites, Derivadas e Integrais
-
- cálculo diferencial e integral II
por Luiz vicente » Seg Mar 06, 2017 13:30
- 0 Respostas
- 5761 Exibições
- Última mensagem por Luiz vicente

Seg Mar 06, 2017 13:30
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Diferencial e Integral I] Limite - Urgente!
por Pessoa Estranha » Ter Mai 27, 2014 23:34
- 2 Respostas
- 2433 Exibições
- Última mensagem por Pessoa Estranha

Qua Mai 28, 2014 22:45
Cálculo: Limites, Derivadas e Integrais
-
- Integral x diferencial!
por Russman » Qua Mai 23, 2012 18:49
- 5 Respostas
- 2637 Exibições
- Última mensagem por Russman

Dom Mai 27, 2012 19:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 107 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
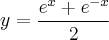 em
em  ".
".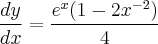
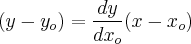
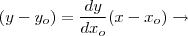
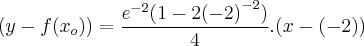
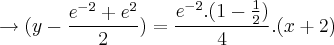
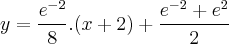
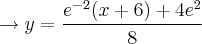
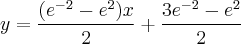


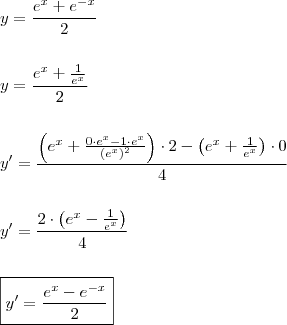
 é dada por
é dada por 
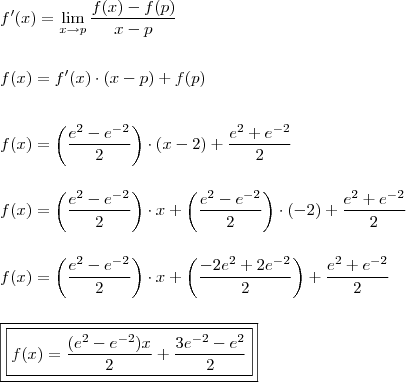


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.