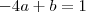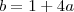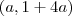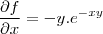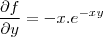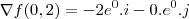por leoflnhs » Seg Set 08, 2014 03:22
por leoflnhs » Seg Set 08, 2014 03:22
-
leoflnhs
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Set 08, 2014 02:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Qua Set 10, 2014 16:12
por young_jedi » Qua Set 10, 2014 16:12
Oque acontece e que todas as direções que satisfazem essa equação são soluções do problema
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por leoflnhs » Qua Set 10, 2014 23:23
por leoflnhs » Qua Set 10, 2014 23:23
Mas teria alguma fórmula que pudesse explicitar todas essas direções?
Encontrei esse problema no livro de Calculo do Stewart vol. 2 (6ª ed.), na página 875, exercicio 28.
-
leoflnhs
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Set 08, 2014 02:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Qui Set 11, 2014 00:10
por young_jedi » Qui Set 11, 2014 00:10
Você poderia fazer
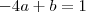
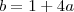
portanto todos os vetores do tipo
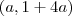
satisfazem o problema
e da uma conferida na derivada parcial pois
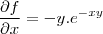
e
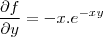
portanto
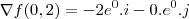
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por leoflnhs » Qui Set 11, 2014 01:06
por leoflnhs » Qui Set 11, 2014 01:06
-
leoflnhs
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Seg Set 08, 2014 02:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2265 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Interpretação de derivadas e funções
por vinik1 » Qua Out 12, 2011 16:03
- 5 Respostas
- 7486 Exibições
- Última mensagem por vinik1

Qui Out 13, 2011 10:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas em pontos dados
por MarlonMO250 » Sex Mar 01, 2013 21:02
- 6 Respostas
- 4965 Exibições
- Última mensagem por Russman

Sáb Mar 02, 2013 03:42
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2974 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Derivadas com definição de limites
 por concurseironf » Sex Set 05, 2014 18:11
por concurseironf » Sex Set 05, 2014 18:11
- 1 Respostas
- 1999 Exibições
- Última mensagem por DanielFerreira

Dom Set 07, 2014 22:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\[f(x,y)= e^{-xy}\] \[f(x,y)= e^{-xy}\]](/latexrender/pictures/b6474f528d0622be5ef02fd1e90a0a94.png) no ponto (0,2) tem valor 1.
no ponto (0,2) tem valor 1.![\[D_{u}f(x,y)=1 \rightarrow grad f(x,y)\cdot <a,b> = 1\] \[D_{u}f(x,y)=1 \rightarrow grad f(x,y)\cdot <a,b> = 1\]](/latexrender/pictures/669f91ff8d72082fb1b1f16ae135ffac.png)
![\[grad f(x,y) = \frac{\partial f}{\partial x}i + \frac{\partial f}{\partial x}j\] \[grad f(x,y) = \frac{\partial f}{\partial x}i + \frac{\partial f}{\partial x}j\]](/latexrender/pictures/813d192820a088667434ef7fd9b033d7.png)
![\[gradf(x,y)=-y^{2}e^{-xy}i+e^{-xy}(1-x)j\] \[gradf(x,y)=-y^{2}e^{-xy}i+e^{-xy}(1-x)j\]](/latexrender/pictures/35636b21998d27aec70af8c0f7a28600.png)
![\[gradf(0,2)=-2^{2}e^{-0*2}i+e^{-0*2}(1-0)j = -4i+j = <-4,1>\] \[gradf(0,2)=-2^{2}e^{-0*2}i+e^{-0*2}(1-0)j = -4i+j = <-4,1>\]](/latexrender/pictures/f96b93e0c29fdbf8456ea918e651aaaa.png)
![\[<-4,1>\cdot <a,b>=1\] \[<-4,1>\cdot <a,b>=1\]](/latexrender/pictures/ff51a6d0d5935f4878981bc293538370.png)
![\[-4a+b=1\] \[-4a+b=1\]](/latexrender/pictures/f8285dbbcd312c017d34bc2afa47e260.png)