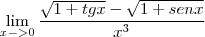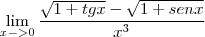por Fernandobertolaccini » Seg Jul 28, 2014 13:38
por Fernandobertolaccini » Seg Jul 28, 2014 13:38
Calcule:
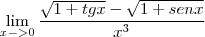
Resp: (1/4)
Muito obrigado !!!
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por young_jedi » Qua Jul 30, 2014 19:38
por young_jedi » Qua Jul 30, 2014 19:38
estou com problemas no editor Latex aqui por isso não estou conseguindo posta a resposta então segue o codigo dela e uma imagem da solução
quando o problema for resolvido alguem por favor conserte o meu post
- Código: Selecionar todos
[tex]\lim_{x \to 0}\frac{\sqrt{1+tg(x)}-\sqrt{1+sen(x)}}{x^3}[/tex]
[tex]\lim_{x \to 0}\frac{\sqrt{1+tg(x)}-\sqrt{1+sen(x)}}{x^3}.\frac{\sqrt{1+tg(x)}+\sqrt{1+sen(x)}}{\sqrt{1+tg(x)}+\sqrt{1+sen(x)}}[/tex]
[tex]\lim_{x \to 0}\frac{1+tg(x)-1-sen(x)}{x^3(\sqrt{1+tg(x)}+\sqrt{1+sen(x)})}[/tex]
[tex]\lim_{x \to 0}\frac{tg(x)-sen(x)}{x^3(\sqrt{1+tg(x)}+\sqrt{1+sen(x)})}[/tex]
[tex]\lim_{x \to 0}\frac{\frac{sen(x)}{cos(x)}-sen(x)}{x^3(\sqrt{1+tg(x)}+\sqrt{1+sen(x)})}[/tex]
[tex]\lim_{x \to 0}\frac{\frac{sen(x)-sen(x)cos(x)}{cos(x)}}{x^3(\sqrt{1+tg(x)}+\sqrt{1+sen(x)})}[/tex]
[attachment=0]latex-23879.png[/attachment]
[tex]\lim_{x \to 0}\frac{sen(x)(1-cos(x))}{cos(x).x^3(\sqrt{1+tg(x)}+\sqrt{1+sen(x)})}[/tex]
[tex]\lim_{x \to 0}\frac{sen(x)(1-cos(x))}{cos(x).x^3(\sqrt{1+tg(x)}+\sqrt{1+sen(x)})}.\frac{1+cos(x)}{1+cos(x)}[/tex]
[tex]\lim_{x \to 0}\frac{sen(x)(1-cos^2(x))}{cos(x).x^3(\sqrt{1+tg(x)}+\sqrt{1+sen(x)})(1+cos(x))}[/tex]
[tex]\lim_{x \to 0}\frac{sen(x)sen^2(x)}{cos(x).x^3(\sqrt{1+tg(x)}+\sqrt{1+sen(x)})(1+cos(x))}[/tex]
[tex]\lim_{x \to 0}\frac{sen^3(x)}{cos(x).x^3(\sqrt{1+tg(x)}+\sqrt{1+sen(x)})(1+cos(x))}[/tex]
[tex]\lim_{x \to 0}\left(\frac{sen(x)}{x}\right)^3\frac{1}{cos(x)(\sqrt{1+tg(x)}+\sqrt{1+sen(x)})(1+cos(x))}=1^3\frac{1}{1(\sqrt{1+0}+\sqrt{1+0})(1+1)}[/tex]
- Anexos
-

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6484 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4566 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 4863 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7044 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4275 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.