 por Fernandobertolaccini » Seg Jul 14, 2014 23:03
por Fernandobertolaccini » Seg Jul 14, 2014 23:03
O tempo que leva um corpo para percorrer, sem atrito, um plano inclinado de inclinação ? e base b é dado pela fórmula
![\sqrt[]{\frac{4b}{gsen2\alpha}} \sqrt[]{\frac{4b}{gsen2\alpha}}](/latexrender/pictures/6a7d44115bb0d8519396011bc53dbfa5.png)
onde g é a aceleração da gravidade.
Determinar ? de modo que t seja mínimo.
Resp: ? = 45º
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por e8group » Qua Jul 16, 2014 00:43
por e8group » Qua Jul 16, 2014 00:43
Uma forma ... Note que
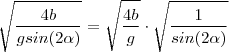
e
![sin(2 \alpha) \in (0,1] sin(2 \alpha) \in (0,1]](/latexrender/pictures/98b63ea3331c741909df9c4a7855e192.png)
o que implica que
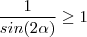
. Vemos que o menor valor que
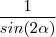
assume é

; ocorrendo quando
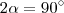
,i.e ,
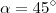
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aplicação de máximos e minimos
por Fernandobertolaccini » Seg Jul 14, 2014 22:48
- 0 Respostas
- 1519 Exibições
- Última mensagem por Fernandobertolaccini

Seg Jul 14, 2014 22:48
Cálculo: Limites, Derivadas e Integrais
-
- Aplicação de máximos e minimos
por Fernandobertolaccini » Seg Jul 14, 2014 22:55
- 1 Respostas
- 1348 Exibições
- Última mensagem por e8group

Ter Jul 15, 2014 14:07
Cálculo: Limites, Derivadas e Integrais
-
- Aplicação de máximos e minimos
por Fernandobertolaccini » Seg Jul 14, 2014 22:50
- 0 Respostas
- 663 Exibições
- Última mensagem por Fernandobertolaccini

Seg Jul 14, 2014 22:50
Cálculo: Limites, Derivadas e Integrais
-
- Aplicação de máximos e minimos
por Fernandobertolaccini » Seg Jul 14, 2014 23:00
- 0 Respostas
- 618 Exibições
- Última mensagem por Fernandobertolaccini

Seg Jul 14, 2014 23:00
Cálculo: Limites, Derivadas e Integrais
-
- [maximos e minimos] Problemas de minimos e maximos
por amigao » Seg Jun 24, 2013 22:28
- 1 Respostas
- 3715 Exibições
- Última mensagem por young_jedi

Ter Jun 25, 2013 17:49
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{\frac{4b}{gsen2\alpha}} \sqrt[]{\frac{4b}{gsen2\alpha}}](/latexrender/pictures/6a7d44115bb0d8519396011bc53dbfa5.png) onde g é a aceleração da gravidade.
onde g é a aceleração da gravidade. 
![\sqrt[]{\frac{4b}{gsen2\alpha}} \sqrt[]{\frac{4b}{gsen2\alpha}}](/latexrender/pictures/6a7d44115bb0d8519396011bc53dbfa5.png) onde g é a aceleração da gravidade.
onde g é a aceleração da gravidade. 
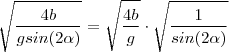 e
e ![sin(2 \alpha) \in (0,1] sin(2 \alpha) \in (0,1]](/latexrender/pictures/98b63ea3331c741909df9c4a7855e192.png) o que implica que
o que implica que 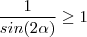 . Vemos que o menor valor que
. Vemos que o menor valor que 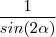 assume é
assume é  ; ocorrendo quando
; ocorrendo quando 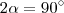 ,i.e ,
,i.e ,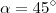 .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.