 por Janoca » Seg Jul 14, 2014 18:45
por Janoca » Seg Jul 14, 2014 18:45
Se uma função tem derivada crescente, então:
a) ela é inversível;
b) sua derivada é positiva;
c) a função é crescente;
d) a função tem ponto de máximo;
e) todas alternativas são falsas.
Gostaria de entender o pq de cada alternativa incorreta e a o motivo da correta.
desde agradeço!
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por e8group » Ter Jul 15, 2014 13:38
por e8group » Ter Jul 15, 2014 13:38
Defina
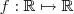
que a cada
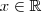
associar um
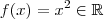
. Note que
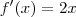
e facilmente verifica-se que
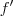
é crescente (neste caso estritamente crescente ) .Agora ...
(I) A função f não é inversível (pois não é injetora , muito menos sobrejetora ) o que implica (a) falso .
(ii) A derivada de f não preservar o sinal ,portanto não positiva o que implica (b) falso.
(iii) Qualquer um dos itens acima implicam que f não é crescente o que implica (c) falso .
(iv) A função não atinge valor máximo . Note que dado qualquer M > 0 o quão grande vc queira temos sempre um f(x) > M ; para tal basta que x seja superior que
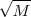
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PA crescente
por jose henrique » Dom Set 19, 2010 12:23
- 2 Respostas
- 3567 Exibições
- Última mensagem por MarceloFantini

Seg Set 20, 2010 03:14
Sequências
-
- PG Crescente
por Lana Brasil » Seg Mai 27, 2019 21:21
- 2 Respostas
- 5513 Exibições
- Última mensagem por Lana Brasil

Qua Mai 29, 2019 09:45
Progressões
-
- [PG infinita e crescente]
por JKS » Qui Abr 11, 2013 01:38
- 1 Respostas
- 2098 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 12:52
Progressões
-
- [PG infinita e crescente]
por JKS » Qui Abr 11, 2013 01:38
- 1 Respostas
- 1889 Exibições
- Última mensagem por DanielFerreira

Ter Abr 16, 2013 12:49
Progressões
-
- Prova de função crescente.
por TheoFerraz » Seg Mai 16, 2011 20:39
- 1 Respostas
- 2721 Exibições
- Última mensagem por LuizAquino

Qua Mai 18, 2011 12:34
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


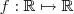 que a cada
que a cada 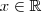 associar um
associar um 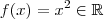 . Note que
. Note que 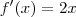 e facilmente verifica-se que
e facilmente verifica-se que 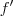 é crescente (neste caso estritamente crescente ) .Agora ...
é crescente (neste caso estritamente crescente ) .Agora ... 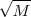 .
.