 por luisbaixo » Dom Jun 29, 2014 16:56
por luisbaixo » Dom Jun 29, 2014 16:56
Fala pessoal tudo bem? Então , eu to com dificuldade pra enxergar a recursividade dessa integral para a transformada cosseno de fourier
Fc(e^-x) o resultado deve ser :(2/pi)*(e^-x)*(-cos(wx)+w*sen(wx))/(1+w²) = (2/pi)^1/2*1/(1+w²)
entretanto eu travei aqui :
![\sqrt[2]{2/pi}*[-{e}^{-x}*cos(wx)-w*{e}^{-x}*sen(wx)+{w}^{2}\int_{0}^\infty e^{-x}*cos(wx)dx \sqrt[2]{2/pi}*[-{e}^{-x}*cos(wx)-w*{e}^{-x}*sen(wx)+{w}^{2}\int_{0}^\infty e^{-x}*cos(wx)dx](/latexrender/pictures/fcb38aee1d77a94daac50d67ed9d29c5.png)
nao consigo enxergar como isso vai ser recursivo , pra mim o grau vai apenas aumentando... , obrigado!!
-
luisbaixo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mai 09, 2014 01:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Dom Jun 29, 2014 18:11
por e8group » Dom Jun 29, 2014 18:11
Para a transformação Fourier ser puramente de cossenos , a aplicação f não deveria ser par ?
E outra ....Não acha mais simples usar a definição
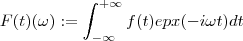
já que estar a trabalhar com
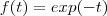
?
De qualquer forma ...Deixo uma dica para computar integrais da forma
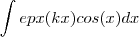
.
Fixe
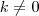
.
Deixe
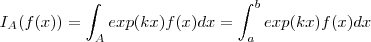
e
![D I_A(f(x)) = \left[exp(kx) f(x)\right]_{a}^b D I_A(f(x)) = \left[exp(kx) f(x)\right]_{a}^b](/latexrender/pictures/db25052bfc895c88168db897e0e06c6d.png)
.
Por partes , tem-se que (com
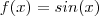
)
![I_A( sin(x)) = \int_A exp(kx) sin(x) dx = \frac{1}{k} \int_A \left(\frac{d}{dx}[ exp(kx)sin(x) ] - exp(kx)cos(x) \right) dx = \frac{1}{k} DI_A(sin(x)) - \frac{1}{k} I_A(cos(x)) I_A( sin(x)) = \int_A exp(kx) sin(x) dx = \frac{1}{k} \int_A \left(\frac{d}{dx}[ exp(kx)sin(x) ] - exp(kx)cos(x) \right) dx = \frac{1}{k} DI_A(sin(x)) - \frac{1}{k} I_A(cos(x))](/latexrender/pictures/475b2b2989642381fdf0800d653ae7e9.png)
.
Aplicando a fórmula acima ,
![I_A( cos(x)) = \int_A exp(kx) cos(x) dx = \frac{1}{k} \int_A \left(\frac{d}{dx}[ exp(kx)cos(x) ] + exp(kx)sin(x) \right) dx = \frac{1}{k} DI_A(cos(x)) +\frac{1}{k} I_A(sin(x)) I_A( cos(x)) = \int_A exp(kx) cos(x) dx = \frac{1}{k} \int_A \left(\frac{d}{dx}[ exp(kx)cos(x) ] + exp(kx)sin(x) \right) dx = \frac{1}{k} DI_A(cos(x)) +\frac{1}{k} I_A(sin(x))](/latexrender/pictures/e55cbbc6206f288eeb8aa9c21c4cb0b4.png)
.
E com isso tem-se o sistema
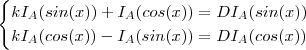
.
Resolvendo encontrará o que se pede . Basta fazer primeiro uma subs. simples
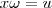
e depois tomar
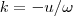
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por luisbaixo » Ter Jul 01, 2014 11:00
por luisbaixo » Ter Jul 01, 2014 11:00
Obrigado cara , ajudou bastante! Mas agora tenho outra dúvida.
Estou com dúvida na parte de modelagem de EDP's , especificamente na parte da equação da onda. Estou com o seguinte problema
Encontre u(x,t) para a corda de comprimento L = 1 e c² = 1 quando a velocidade inicial for zero e a deflexão inicial com pequenos valores de k (digamos 0,01) for como se segue.
2)k(sen(pi*x) - (1/3)*sen(3*pi*x))
4)kx(1-x²)
O negócio é que eu sei que tenho que usar U(x,o) = E(Bn*sen(n*pi*x/L)) mas só isso(nem o Bn eu to entendendo mais haha) , nao sei como fazer o resto estou realmente perdido =/
E sei também que o u(x,t) = E(Bn*cos(at)+Bn*sen(at))*sen(n*pi*x/L) e que a = lambda = c*n*pi/L , certo?
Obrigado!
-
luisbaixo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sex Mai 09, 2014 01:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Serie de Fourier
 por Thaila » Qua Jul 20, 2011 20:08
por Thaila » Qua Jul 20, 2011 20:08
- 1 Respostas
- 1736 Exibições
- Última mensagem por MarceloFantini

Qui Jul 21, 2011 01:46
Sequências
-
- Series de Fourier
por 380625 » Qua Set 28, 2011 01:30
- 1 Respostas
- 1543 Exibições
- Última mensagem por Neperiano

Qua Set 28, 2011 15:21
Sequências
-
- Series de Fourier. Urgente.
por 380625 » Qui Set 29, 2011 11:39
- 0 Respostas
- 1097 Exibições
- Última mensagem por 380625

Qui Set 29, 2011 11:39
Sequências
-
- Duvida em série de Fourier
por luisbaixo » Sex Mai 09, 2014 01:22
- 7 Respostas
- 4823 Exibições
- Última mensagem por Russman

Sáb Mai 10, 2014 22:00
Cálculo: Limites, Derivadas e Integrais
-
- Séries de Fourier de Funções Hiperbólicas
 por clecio » Qua Abr 13, 2011 14:18
por clecio » Qua Abr 13, 2011 14:18
- 1 Respostas
- 2225 Exibições
- Última mensagem por LuizAquino

Qui Abr 14, 2011 23:32
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{2/pi}*[-{e}^{-x}*cos(wx)-w*{e}^{-x}*sen(wx)+{w}^{2}\int_{0}^\infty e^{-x}*cos(wx)dx \sqrt[2]{2/pi}*[-{e}^{-x}*cos(wx)-w*{e}^{-x}*sen(wx)+{w}^{2}\int_{0}^\infty e^{-x}*cos(wx)dx](/latexrender/pictures/fcb38aee1d77a94daac50d67ed9d29c5.png)

![\sqrt[2]{2/pi}*[-{e}^{-x}*cos(wx)-w*{e}^{-x}*sen(wx)+{w}^{2}\int_{0}^\infty e^{-x}*cos(wx)dx \sqrt[2]{2/pi}*[-{e}^{-x}*cos(wx)-w*{e}^{-x}*sen(wx)+{w}^{2}\int_{0}^\infty e^{-x}*cos(wx)dx](/latexrender/pictures/fcb38aee1d77a94daac50d67ed9d29c5.png)

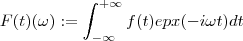 já que estar a trabalhar com
já que estar a trabalhar com 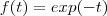 ?
? 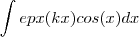 .
. 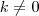 .
.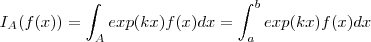 e
e ![D I_A(f(x)) = \left[exp(kx) f(x)\right]_{a}^b D I_A(f(x)) = \left[exp(kx) f(x)\right]_{a}^b](/latexrender/pictures/db25052bfc895c88168db897e0e06c6d.png) .
. 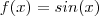 )
)![I_A( sin(x)) = \int_A exp(kx) sin(x) dx = \frac{1}{k} \int_A \left(\frac{d}{dx}[ exp(kx)sin(x) ] - exp(kx)cos(x) \right) dx = \frac{1}{k} DI_A(sin(x)) - \frac{1}{k} I_A(cos(x)) I_A( sin(x)) = \int_A exp(kx) sin(x) dx = \frac{1}{k} \int_A \left(\frac{d}{dx}[ exp(kx)sin(x) ] - exp(kx)cos(x) \right) dx = \frac{1}{k} DI_A(sin(x)) - \frac{1}{k} I_A(cos(x))](/latexrender/pictures/475b2b2989642381fdf0800d653ae7e9.png) .
. ![I_A( cos(x)) = \int_A exp(kx) cos(x) dx = \frac{1}{k} \int_A \left(\frac{d}{dx}[ exp(kx)cos(x) ] + exp(kx)sin(x) \right) dx = \frac{1}{k} DI_A(cos(x)) +\frac{1}{k} I_A(sin(x)) I_A( cos(x)) = \int_A exp(kx) cos(x) dx = \frac{1}{k} \int_A \left(\frac{d}{dx}[ exp(kx)cos(x) ] + exp(kx)sin(x) \right) dx = \frac{1}{k} DI_A(cos(x)) +\frac{1}{k} I_A(sin(x))](/latexrender/pictures/e55cbbc6206f288eeb8aa9c21c4cb0b4.png) .
.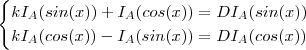 .
.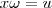 e depois tomar
e depois tomar 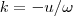 .
.

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
