-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 480522 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 541182 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 504977 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 731912 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2173198 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por Janoca » Dom Jun 22, 2014 02:40
por Janoca » Dom Jun 22, 2014 02:40
Questão:
Suponha que
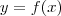
seja uma função derivável dada implicitamente pela equação
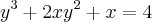
. suponha, ainda, que
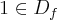
.
a) Calcule
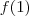
.
b) Determine a equação da reta tangente ao gráfico de f no ponto de abscissa 1.
Não consigo resolver, pq a letra a é igual a 1. eu sei como resolver a reta tangente, mas como não entendi o f(1), não da de fazer a letra b.
Ajudem-me
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por e8group » Dom Jun 22, 2014 12:57
por e8group » Dom Jun 22, 2014 12:57
Não conseguiu ? Talvez conseguiste , check a resolução abaixo .
A reta requerida passa pelo ponto
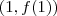
e seu coeficiente angular é
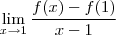
que igual a
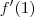
se o
limite for finito e existir; se dê infinito, bem provável que esta reta é perpendicular à reta
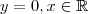
(eixo x) e se for finito , em particular zero , esta reta será paralela ao eixo x . Tô dizendo isso , por que estas duas situações podem ocorrer . Segue de (a) ,
![[y^3 +2xy^2 +x]' = 0 [y^3 +2xy^2 +x]' = 0](/latexrender/pictures/82db009061458b5952b2a7a47d670ef2.png)
\iff

.
Levando em conta que seus cálculos estão certos
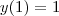
,
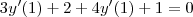
\iff [/tex] 7 y'(1) + 3 = 0 [/tex] \iff
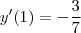
.
Da forma que você se expressou , pensei que uma daquelas situações tinha ocorrido , mas não .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Janoca » Ter Jun 24, 2014 16:52
por Janoca » Ter Jun 24, 2014 16:52
Obrigada pela dica, de fato consegui fazer a questão.
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por jugrigori » Dom Jun 03, 2018 16:05
por jugrigori » Dom Jun 03, 2018 16:05
Eu não entendi a questão, como eu encontro o f(1)?
-
jugrigori
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mai 10, 2018 20:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada Implícita
por ariclenesmelo » Ter Out 23, 2012 14:32
- 3 Respostas
- 2530 Exibições
- Última mensagem por young_jedi

Qui Out 25, 2012 22:33
Cálculo: Limites, Derivadas e Integrais
-
- [derivada implícita]exercício
por luiz_henriquear » Seg Out 24, 2011 20:48
- 5 Respostas
- 3660 Exibições
- Última mensagem por LuizAquino

Ter Nov 01, 2011 23:04
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Função Implicita
por fabriel » Sex Mar 15, 2013 13:27
- 1 Respostas
- 1300 Exibições
- Última mensagem por e8group

Sex Mar 15, 2013 21:50
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida - derivada implícita
por Danilo » Dom Out 13, 2013 22:31
- 2 Respostas
- 1659 Exibições
- Última mensagem por Danilo

Seg Out 14, 2013 01:32
Cálculo: Limites, Derivadas e Integrais
-
- Derivada implicita, provar resultado
por rodrigo lara » Sáb Jan 04, 2014 17:53
- 5 Respostas
- 3946 Exibições
- Última mensagem por rodrigo lara

Qua Jan 08, 2014 13:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 60 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
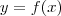 seja uma função derivável dada implicitamente pela equação
seja uma função derivável dada implicitamente pela equação 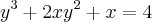 . suponha, ainda, que
. suponha, ainda, que 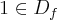 .
.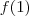 .
.

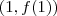 e seu coeficiente angular é
e seu coeficiente angular é 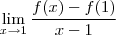 que igual a
que igual a 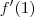 se o
se o 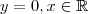 (eixo x) e se for finito , em particular zero , esta reta será paralela ao eixo x . Tô dizendo isso , por que estas duas situações podem ocorrer . Segue de (a) ,
(eixo x) e se for finito , em particular zero , esta reta será paralela ao eixo x . Tô dizendo isso , por que estas duas situações podem ocorrer . Segue de (a) , ![[y^3 +2xy^2 +x]' = 0 [y^3 +2xy^2 +x]' = 0](/latexrender/pictures/82db009061458b5952b2a7a47d670ef2.png) \iff
\iff  .
. 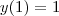 ,
, 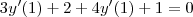 \iff [/tex] 7 y'(1) + 3 = 0 [/tex] \iff
\iff [/tex] 7 y'(1) + 3 = 0 [/tex] \iff 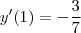 .
.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.