 por Janoca » Dom Jun 22, 2014 02:40
por Janoca » Dom Jun 22, 2014 02:40
Questão:
Suponha que
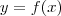
seja uma função derivável dada implicitamente pela equação
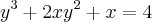
. suponha, ainda, que
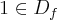
.
a) Calcule
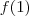
.
b) Determine a equação da reta tangente ao gráfico de f no ponto de abscissa 1.
Não consigo resolver, pq a letra a é igual a 1. eu sei como resolver a reta tangente, mas como não entendi o f(1), não da de fazer a letra b.
Ajudem-me
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por e8group » Dom Jun 22, 2014 12:57
por e8group » Dom Jun 22, 2014 12:57
Não conseguiu ? Talvez conseguiste , check a resolução abaixo .
A reta requerida passa pelo ponto
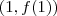
e seu coeficiente angular é
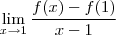
que igual a
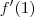
se o limite for finito e existir; se dê infinito, bem provável que esta reta é perpendicular à reta
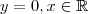
(eixo x) e se for finito , em particular zero , esta reta será paralela ao eixo x . Tô dizendo isso , por que estas duas situações podem ocorrer . Segue de (a) ,
![[y^3 +2xy^2 +x]' = 0 [y^3 +2xy^2 +x]' = 0](/latexrender/pictures/82db009061458b5952b2a7a47d670ef2.png)
\iff

.
Levando em conta que seus cálculos estão certos
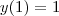
,
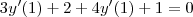
\iff [/tex] 7 y'(1) + 3 = 0 [/tex] \iff
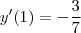
.
Da forma que você se expressou , pensei que uma daquelas situações tinha ocorrido , mas não .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Janoca » Ter Jun 24, 2014 16:52
por Janoca » Ter Jun 24, 2014 16:52
Obrigada pela dica, de fato consegui fazer a questão.
-
Janoca
- Usuário Dedicado

-
- Mensagens: 30
- Registrado em: Sex Jun 06, 2014 16:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por jugrigori » Dom Jun 03, 2018 16:05
por jugrigori » Dom Jun 03, 2018 16:05
Eu não entendi a questão, como eu encontro o f(1)?
-
jugrigori
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mai 10, 2018 20:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada Implícita
por ariclenesmelo » Ter Out 23, 2012 14:32
- 3 Respostas
- 2787 Exibições
- Última mensagem por young_jedi

Qui Out 25, 2012 22:33
Cálculo: Limites, Derivadas e Integrais
-
- [derivada implícita]exercício
por luiz_henriquear » Seg Out 24, 2011 20:48
- 5 Respostas
- 4118 Exibições
- Última mensagem por LuizAquino

Ter Nov 01, 2011 23:04
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Função Implicita
por fabriel » Sex Mar 15, 2013 13:27
- 1 Respostas
- 1537 Exibições
- Última mensagem por e8group

Sex Mar 15, 2013 21:50
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida - derivada implícita
por Danilo » Dom Out 13, 2013 22:31
- 2 Respostas
- 1925 Exibições
- Última mensagem por Danilo

Seg Out 14, 2013 01:32
Cálculo: Limites, Derivadas e Integrais
-
- Derivada implicita, provar resultado
por rodrigo lara » Sáb Jan 04, 2014 17:53
- 5 Respostas
- 4391 Exibições
- Última mensagem por rodrigo lara

Qua Jan 08, 2014 13:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
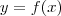 seja uma função derivável dada implicitamente pela equação
seja uma função derivável dada implicitamente pela equação 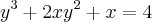 . suponha, ainda, que
. suponha, ainda, que 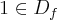 .
.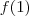 .
.

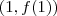 e seu coeficiente angular é
e seu coeficiente angular é 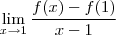 que igual a
que igual a 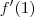 se o limite for finito e existir; se dê infinito, bem provável que esta reta é perpendicular à reta
se o limite for finito e existir; se dê infinito, bem provável que esta reta é perpendicular à reta 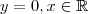 (eixo x) e se for finito , em particular zero , esta reta será paralela ao eixo x . Tô dizendo isso , por que estas duas situações podem ocorrer . Segue de (a) ,
(eixo x) e se for finito , em particular zero , esta reta será paralela ao eixo x . Tô dizendo isso , por que estas duas situações podem ocorrer . Segue de (a) , ![[y^3 +2xy^2 +x]' = 0 [y^3 +2xy^2 +x]' = 0](/latexrender/pictures/82db009061458b5952b2a7a47d670ef2.png) \iff
\iff  .
. 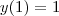 ,
, 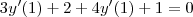 \iff [/tex] 7 y'(1) + 3 = 0 [/tex] \iff
\iff [/tex] 7 y'(1) + 3 = 0 [/tex] \iff 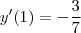 .
.






