 por nievag » Ter Mai 13, 2014 00:58
por nievag » Ter Mai 13, 2014 00:58
No livro de James Stewart a resposta é 5, alguém consegue provar isso através do teorema do confronto?

-
nievag
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mai 13, 2014 00:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por e8group » Ter Mai 13, 2014 10:50
por e8group » Ter Mai 13, 2014 10:50
P/a função seno avaliados em valores suficientemente pequenos , digamos

, temos que
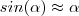
. Este fato é evidente , do ponto de vista geométrico . Dá circunferência unitária vemos que o valor real de

difere pouco de

(compare

com a projeção do mesmo sobre o eixo ) . Observe que para x grande (positivamente ou negativamente ) , a nossa expectativa é que

isto nos leva a

. Quanto vale o limite ? Este limite tem alguma relação com o limite fundamental envolvendo o seno ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [limite]teorema do confronto
por gabriel feron » Dom Mai 06, 2012 20:25
- 1 Respostas
- 1821 Exibições
- Última mensagem por MarceloFantini

Dom Mai 06, 2012 22:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limimite] Limite de sequência e teorema do confronto
por Aliocha Karamazov » Qui Set 15, 2011 21:01
- 5 Respostas
- 3187 Exibições
- Última mensagem por MarceloFantini

Sex Set 16, 2011 16:56
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Calculo de limite usando o teorema do confronto.
por erickm93 » Qua Mai 22, 2013 10:48
- 3 Respostas
- 6024 Exibições
- Última mensagem por erickm93

Qua Mai 22, 2013 23:49
Cálculo: Limites, Derivadas e Integrais
-
- limite: demonstração (acho que utiliza teorema do confronto)
por catabluma123 » Qua Fev 10, 2016 21:52
- 1 Respostas
- 1635 Exibições
- Última mensagem por adauto martins

Seg Fev 22, 2016 12:43
Cálculo: Limites, Derivadas e Integrais
-
- Teorema do Confronto
por Claudin » Qua Mai 25, 2011 19:51
- 3 Respostas
- 3439 Exibições
- Última mensagem por LuizAquino

Qua Mai 25, 2011 21:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





 , temos que
, temos que 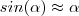 . Este fato é evidente , do ponto de vista geométrico . Dá circunferência unitária vemos que o valor real de
. Este fato é evidente , do ponto de vista geométrico . Dá circunferência unitária vemos que o valor real de  difere pouco de
difere pouco de  (compare
(compare  com a projeção do mesmo sobre o eixo ) . Observe que para x grande (positivamente ou negativamente ) , a nossa expectativa é que
com a projeção do mesmo sobre o eixo ) . Observe que para x grande (positivamente ou negativamente ) , a nossa expectativa é que  isto nos leva a
isto nos leva a  . Quanto vale o limite ? Este limite tem alguma relação com o limite fundamental envolvendo o seno ?
. Quanto vale o limite ? Este limite tem alguma relação com o limite fundamental envolvendo o seno ?

 .
.
 :
: