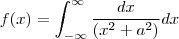 .
.Como fiz levei ela para o campo complexo e depois usei o teorema dos residuos e deu certinho.
Agora quero resolver a seguinte :
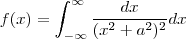
A primeira integral tinha dois polos, agora a segunda tem quatro polos? Dessa forma não sei como usar o teorema dos residuos.
Gostaria de alguma dica ou alguma sugestão.
Primeira solução:
Teremos que:

onde os residuos são dados por:
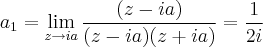
Dessa forma
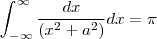
Agora não sei como proceder com a integral abaixo:
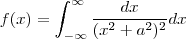


 = integrando ,temos que g satisfaz a propriedade
= integrando ,temos que g satisfaz a propriedade 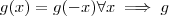 é par .Assim , a integral se resume a
é par .Assim , a integral se resume a 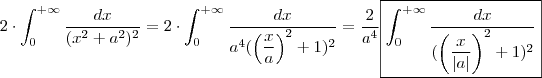 .
. 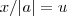 implica
implica 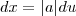 e os limites de intregração
e os limites de intregração  e
e  (qualquer a !=0 ) .
(qualquer a !=0 ) .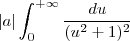 .
. ![|a| \int_{0}^{+\infty} \frac{du}{(u^2+1)^2} = |a| \int_{0}^{+\infty} \frac{1}{u^2+1} \cdot \frac{1}{u^2+1} du = |a| \int_{0}^{+\infty} [arctan(u)]' \cdot \frac{1}{u^2+1} du (*) |a| \int_{0}^{+\infty} \frac{du}{(u^2+1)^2} = |a| \int_{0}^{+\infty} \frac{1}{u^2+1} \cdot \frac{1}{u^2+1} du = |a| \int_{0}^{+\infty} [arctan(u)]' \cdot \frac{1}{u^2+1} du (*)](/latexrender/pictures/e83aeb9acdea866c1b6ba407cb6b8d09.png) .
. 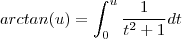 e
e ![[arctan(u)]' = 1/(u^2+1) [arctan(u)]' = 1/(u^2+1)](/latexrender/pictures/8e069ffbb1477567359de5b7961aea95.png)
 temos
temos 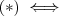
![|a| \int_{0}^{+\infty} \left( \left[\frac{arctan(u)}{u^2+1} \right]' + arctan(u) \cdot \frac{2u}{(u^2+1)^2} \right) |a| \int_{0}^{+\infty} \left( \left[\frac{arctan(u)}{u^2+1} \right]' + arctan(u) \cdot \frac{2u}{(u^2+1)^2} \right)](/latexrender/pictures/5b25853751cc81c64c36f682340e6b3f.png)
![= |a| \left( \left[\frac{arctan(u)}{u^2+1} \right]_0^{+\infty} + \int_0^{+\infty} arctan(u) \cdot \frac{2u}{(u^2+1)^2} du \right) = |a| \left( \left[\frac{arctan(u)}{u^2+1} \right]_0^{+\infty} + \int_0^{+\infty} arctan(u) \cdot \frac{2u}{(u^2+1)^2} du \right)](/latexrender/pictures/ecad933e93dbe1742038e8d1041f7859.png)
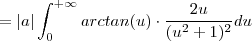 .
.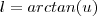 .
. 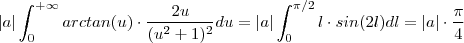 .
.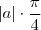 , e assim
, e assim 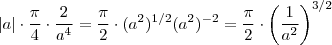 .
.
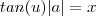 (usando módulo pq não sei se a > 0 ou a < 0 )
(usando módulo pq não sei se a > 0 ou a < 0 ) 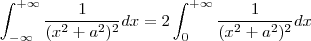 .
. 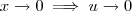 e
e 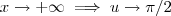 , e além disso
, e além disso 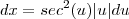 , logo
, logo 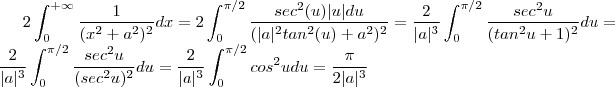 .
. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.