Então comecei a integrar cada uma das expressões acima e criei uma nova tabela:
No entanto, eu desgostei do resultado da integral circulada em vermelho, porque, na verdade, eu não sei transformar a função arctan(...) numa expressão similar às expressões das duas integrais (de cima e de baixo) adjacentes. Eu tentei alguma coisa, vejam:
Mas este resultado não é suficientemente parecido com a integrais de
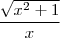e 
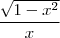.Você tem ideia de como fazer tal integral ser parecida com as demais?
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)